Deep Learning Methods for Partial Differential Equations and Related Parameter Identification Problems

Recent years have witnessed a growth in mathematics for deep learning--which seeks a deeper understanding of the concepts of deep learning with mathematics, and explores how to make it more robust--and deep learning for mathematics, where deep learning algorithms are used to solve problems in mathematics. The latter has popularised the field of scientific machine learning where deep learning is applied to problems in scientific computing. Specifically, more and more neural network architectures have been developed to solve specific classes of partial differential equations (PDEs). Such methods exploit properties that are inherent to PDEs and thus solve the PDEs better than classical feed-forward neural networks, recurrent neural networks, and convolutional neural networks. This has had a great impact in the area of mathematical modeling where parametric PDEs are widely used to model most natural and physical processes arising in science and engineering, In this work, we review such methods and extend them for parametric studies as well as for solving the related inverse problems. We equally proceed to show their relevance in some industrial applications.

Physics-based polynomial neural networks for one-shot learning of dynamical systems from one or a few samples

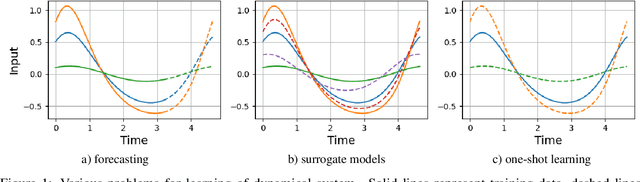
This paper discusses an approach for incorporating prior physical knowledge into the neural network to improve data efficiency and the generalization of predictive models. If the dynamics of a system approximately follows a given differential equation, the Taylor mapping method can be used to initialize the weights of a polynomial neural network. This allows the fine-tuning of the model from one training sample of real system dynamics. The paper describes practical results on real experiments with both a simple pendulum and one of the largest worldwide X-ray source. It is demonstrated in practice that the proposed approach allows recovering complex physics from noisy, limited, and partial observations and provides meaningful predictions for previously unseen inputs. The approach mainly targets the learning of physical systems when state-of-the-art models are difficult to apply given the lack of training data.

Polynomial Neural Networks and Taylor maps for Dynamical Systems Simulation and Learning

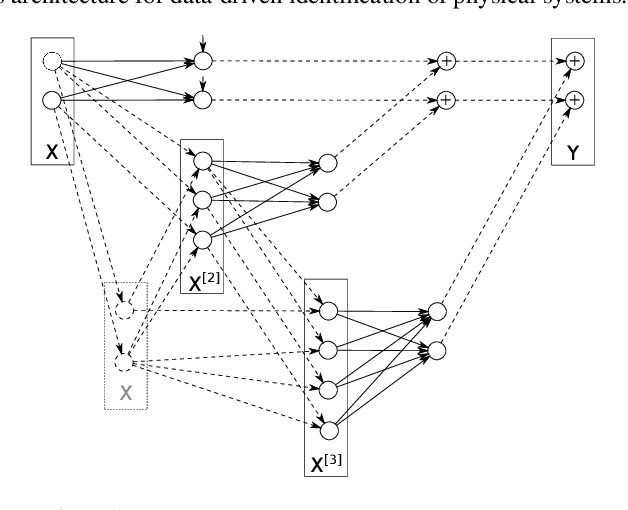
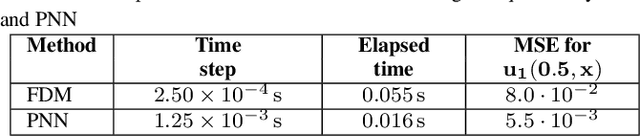
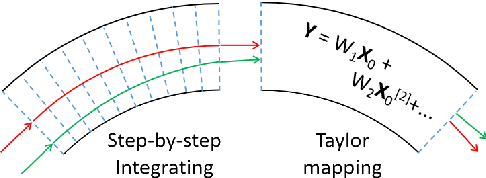
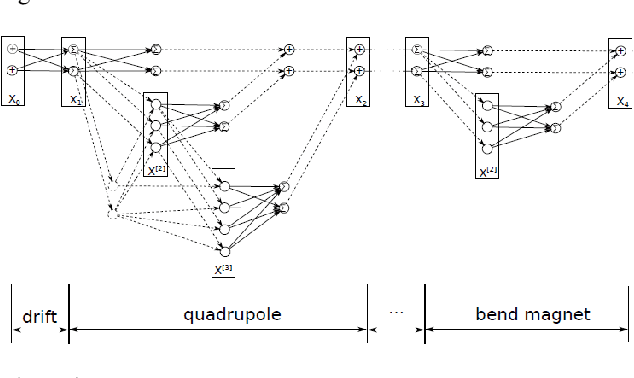
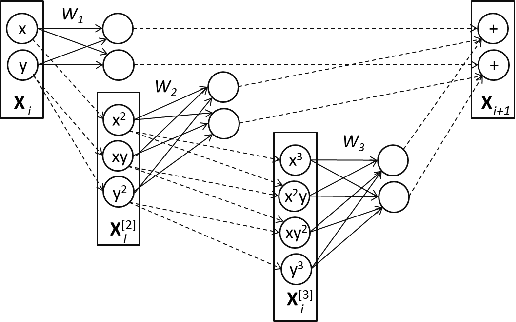
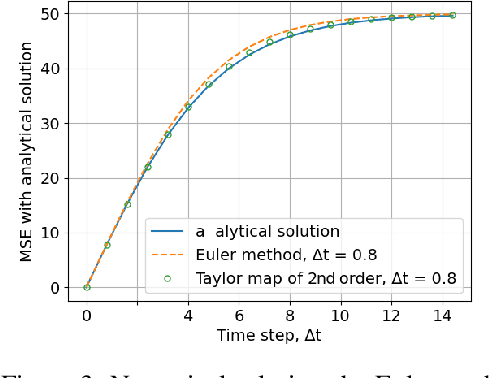
The connection of Taylor maps and polynomial neural networks (PNN) to solve ordinary differential equations (ODEs) numerically is considered. Having the system of ODEs, it is possible to calculate weights of PNN that simulates the dynamics of these equations. It is shown that proposed PNN architecture can provide better accuracy with less computational time in comparison with traditional numerical solvers. Moreover, neural network derived from the ODEs can be used for simulation of system dynamics with different initial conditions, but without training procedure. On the other hand, if the equations are unknown, the weights of the PNN can be fitted in a data-driven way. In the paper we describe the connection of PNN with differential equations in a theoretical way along with the examples for both dynamics simulation and learning with data.