Learning the Evolution of Correlated Stochastic Power System Dynamics

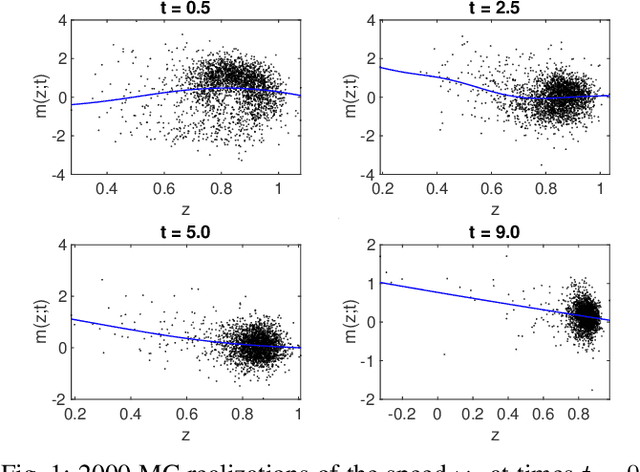
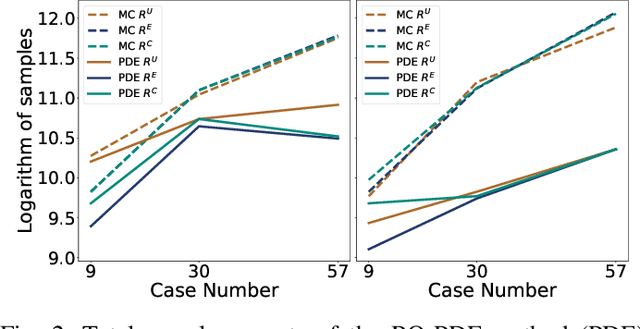
A machine learning technique is proposed for quantifying uncertainty in power system dynamics with spatiotemporally correlated stochastic forcing. We learn one-dimensional linear partial differential equations for the probability density functions of real-valued quantities of interest. The method is suitable for high-dimensional systems and helps to alleviate the curse of dimensionality.

Autonomous learning of nonlocal stochastic neuron dynamics

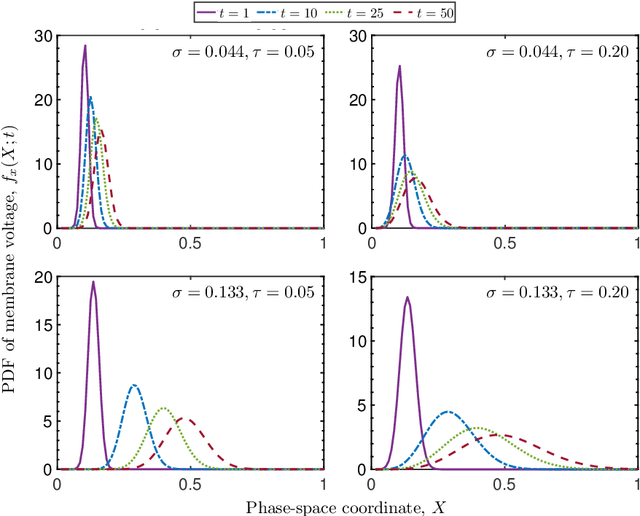
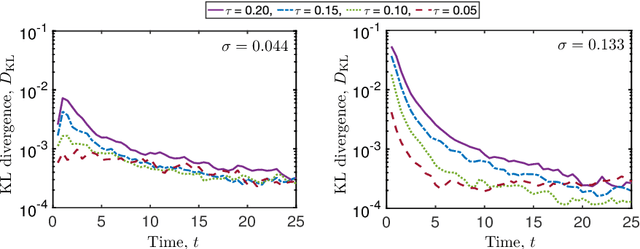
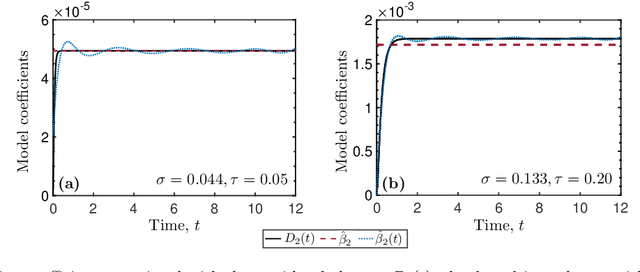
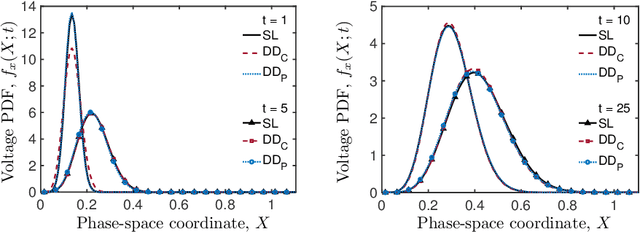
Neuronal dynamics is driven by externally imposed or internally generated random excitations/noise, and is often described by systems of stochastic ordinary differential equations. A solution to these equations is the joint probability density function (PDF) of neuron states. It can be used to calculate such information-theoretic quantities as the mutual information between the stochastic stimulus and various internal states of the neuron (e.g., membrane potential), as well as various spiking statistics. When random excitations are modeled as Gaussian white noise, the joint PDF of neuron states satisfies exactly a Fokker-Planck equation. However, most biologically plausible noise sources are correlated (colored). In this case, the resulting PDF equations require a closure approximation. We propose two methods for closing such equations: a modified nonlocal large-eddy-diffusivity closure and a data-driven closure relying on sparse regression to learn relevant features. The closures are tested for stochastic leaky integrate-and-fire (LIF) and FitzHugh-Nagumo (FHN) neurons driven by sine-Wiener noise. Mutual information and total correlation between the random stimulus and the internal states of the neuron are calculated for the FHN neuron.