Introducing Fractional Classification Loss for Robust Learning with Noisy Labels

Robust loss functions are crucial for training deep neural networks in the presence of label noise, yet existing approaches require extensive, dataset-specific hyperparameter tuning. In this work, we introduce Fractional Classification Loss (FCL), an adaptive robust loss that automatically calibrates its robustness to label noise during training. Built within the active-passive loss framework, FCL employs the fractional derivative of the Cross-Entropy (CE) loss as its active component and the Mean Absolute Error (MAE) as its passive loss component. With this formulation, we demonstrate that the fractional derivative order $\mu$ spans a family of loss functions that interpolate between MAE-like robustness and CE-like fast convergence. Furthermore, we integrate $\mu$ into the gradient-based optimization as a learnable parameter and automatically adjust it to optimize the trade-off between robustness and convergence speed. We reveal that FCL's unique property establishes a critical trade-off that enables the stable learning of $\mu$: lower log penalties on difficult or mislabeled examples improve robustness but impose higher penalties on easy or clean data, reducing model confidence in them. Consequently, FCL can dynamically reshape its loss landscape to achieve effective classification performance under label noise. Extensive experiments on benchmark datasets show that FCL achieves state-of-the-art results without the need for manual hyperparameter tuning.

Redefining Clustered Federated Learning for System Identification: The Path of ClusterCraft

This paper addresses the System Identification (SYSID) problem within the framework of federated learning. We introduce a novel algorithm, Incremental Clustering-based federated learning method for SYSID (IC-SYSID), designed to tackle SYSID challenges across multiple data sources without prior knowledge. IC-SYSID utilizes an incremental clustering method, ClusterCraft (CC), to eliminate the dependency on the prior knowledge of the dataset. CC starts with a single cluster model and assigns similar local workers to the same clusters by dynamically increasing the number of clusters. To reduce the number of clusters generated by CC, we introduce ClusterMerge, where similar cluster models are merged. We also introduce enhanced ClusterCraft to reduce the generation of similar cluster models during the training. Moreover, IC-SYSID addresses cluster model instability by integrating a regularization term into the loss function and initializing cluster models with scaled Glorot initialization. It also utilizes a mini-batch deep learning approach to manage large SYSID datasets during local training. Through the experiments conducted on a real-world representing SYSID problem, where a fleet of vehicles collaboratively learns vehicle dynamics, we show that IC-SYSID achieves a high SYSID performance while preventing the learning of unstable clusters.

Capturing Aerodynamic Characteristics of ATTAS Aircraft with Evolving Intelligent System

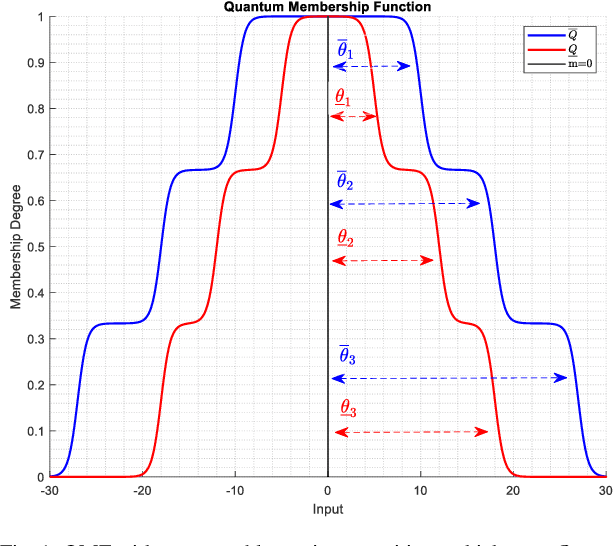
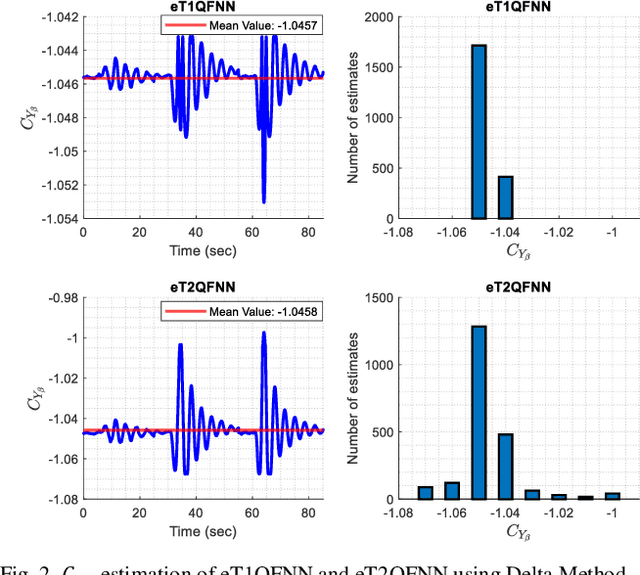
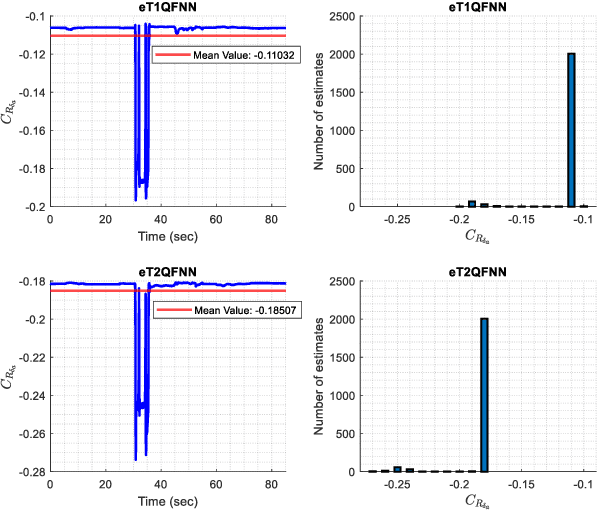
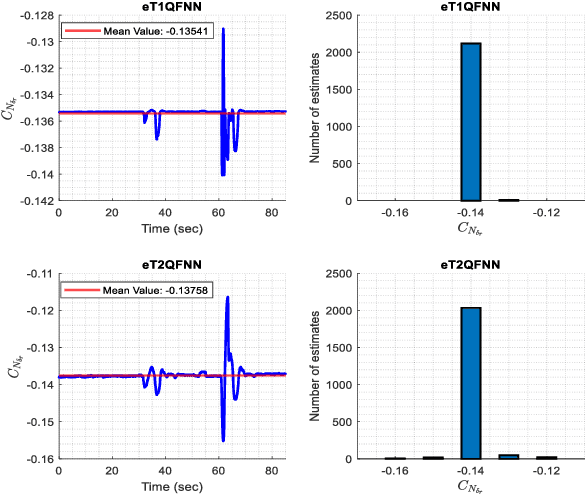
Accurate modeling of aerodynamic coefficients is crucial for understanding and optimizing the performance of modern aircraft systems. This paper presents the novel deployment of an Evolving Type-2 Quantum Fuzzy Neural Network (eT2QFNN) for modeling the aerodynamic coefficients of the ATTAS aircraft to express the aerodynamic characteristics. eT2QFNN can represent the nonlinear aircraft model by creating multiple linear submodels with its rule-based structure through an incremental learning strategy rather than a traditional batch learning approach. Moreover, it enhances robustness to uncertainties and data noise through its quantum membership functions, as well as its automatic rule-learning and parameter-tuning capabilities. During the estimation of the aerodynamic coefficients via the flight data of the ATTAS, two different studies are conducted in the training phase: one with a large amount of data and the other with a limited amount of data. The results show that the modeling performance of the eT2QFNN is superior in comparison to baseline counterparts. Furthermore, eT2QFNN estimated the aerodynamic model with fewer rules compared to Type-1 fuzzy counterparts. In addition, by applying the Delta method to the proposed approach, the stability and control derivatives of the aircraft are analyzed. The results prove the superiority of the proposed eT2QFNN in representing aerodynamic coefficients.

Introducing Interval Neural Networks for Uncertainty-Aware System Identification

System Identification (SysID) is crucial for modeling and understanding dynamical systems using experimental data. While traditional SysID methods emphasize linear models, their inability to fully capture nonlinear dynamics has driven the adoption of Deep Learning (DL) as a more powerful alternative. However, the lack of uncertainty quantification (UQ) in DL-based models poses challenges for reliability and safety, highlighting the necessity of incorporating UQ. This paper introduces a systematic framework for constructing and learning Interval Neural Networks (INNs) to perform UQ in SysID tasks. INNs are derived by transforming the learnable parameters (LPs) of pre-trained neural networks into interval-valued LPs without relying on probabilistic assumptions. By employing interval arithmetic throughout the network, INNs can generate Prediction Intervals (PIs) that capture target coverage effectively. We extend Long Short-Term Memory (LSTM) and Neural Ordinary Differential Equations (Neural ODEs) into Interval LSTM (ILSTM) and Interval NODE (INODE) architectures, providing the mathematical foundations for their application in SysID. To train INNs, we propose a DL framework that integrates a UQ loss function and parameterization tricks to handle constraints arising from interval LPs. We introduce novel concept "elasticity" for underlying uncertainty causes and validate ILSTM and INODE in SysID experiments, demonstrating their effectiveness.

Imitation Learning for Autonomous Driving: Insights from Real-World Testing

This work focuses on the design of a deep learning-based autonomous driving system deployed and tested on the real-world MIT Racecar to assess its effectiveness in driving scenarios. The Deep Neural Network (DNN) translates raw image inputs into real-time steering commands in an end-to-end learning fashion, following the imitation learning framework. The key design challenge is to ensure that DNN predictions are accurate and fast enough, at a high sampling frequency, and result in smooth vehicle operation under different operating conditions. In this study, we design and compare various DNNs, to identify the most effective approach for real-time autonomous driving. In designing the DNNs, we adopted an incremental design approach that involved enhancing the model capacity and dataset to address the challenges of real-world driving scenarios. We designed a PD system, CNN, CNN-LSTM, and CNN-NODE, and evaluated their performance on the real-world MIT Racecar. While the PD system handled basic lane following, it struggled with sharp turns and lighting variations. The CNN improved steering but lacked temporal awareness, which the CNN-LSTM addressed as it resulted in smooth driving performance. The CNN-NODE performed similarly to the CNN-LSTM in handling driving dynamics, yet with slightly better driving performance. The findings of this research highlight the importance of iterative design processes in developing robust DNNs for autonomous driving applications. The experimental video is available at https://www.youtube.com/watch?v=FNNYgU--iaY.

Adapting GT2-FLS for Uncertainty Quantification: A Blueprint Calibration Strategy

Uncertainty Quantification (UQ) is crucial for deploying reliable Deep Learning (DL) models in high-stakes applications. Recently, General Type-2 Fuzzy Logic Systems (GT2-FLSs) have been proven to be effective for UQ, offering Prediction Intervals (PIs) to capture uncertainty. However, existing methods often struggle with computational efficiency and adaptability, as generating PIs for new coverage levels $(\phi_d)$ typically requires retraining the model. Moreover, methods that directly estimate the entire conditional distribution for UQ are computationally expensive, limiting their scalability in real-world scenarios. This study addresses these challenges by proposing a blueprint calibration strategy for GT2-FLSs, enabling efficient adaptation to any desired $\phi_d$ without retraining. By exploring the relationship between $\alpha$-plane type reduced sets and uncertainty coverage, we develop two calibration methods: a lookup table-based approach and a derivative-free optimization algorithm. These methods allow GT2-FLSs to produce accurate and reliable PIs while significantly reducing computational overhead. Experimental results on high-dimensional datasets demonstrate that the calibrated GT2-FLS achieves superior performance in UQ, highlighting its potential for scalable and practical applications.

FAME: Introducing Fuzzy Additive Models for Explainable AI

In this study, we introduce the Fuzzy Additive Model (FAM) and FAM with Explainability (FAME) as a solution for Explainable Artificial Intelligence (XAI). The family consists of three layers: (1) a Projection Layer that compresses the input space, (2) a Fuzzy Layer built upon Single Input-Single Output Fuzzy Logic Systems (SFLS), where SFLS functions as subnetworks within an additive index model, and (3) an Aggregation Layer. This architecture integrates the interpretability of SFLS, which uses human-understandable if-then rules, with the explainability of input-output relationships, leveraging the additive model structure. Furthermore, using SFLS inherently addresses issues such as the curse of dimensionality and rule explosion. To further improve interpretability, we propose a method for sculpting antecedent space within FAM, transforming it into FAME. We show that FAME captures the input-output relationships with fewer active rules, thus improving clarity. To learn the FAM family, we present a deep learning framework. Through the presented comparative results, we demonstrate the promising potential of FAME in reducing model complexity while retaining interpretability, positioning it as a valuable tool for XAI.

A State Alignment-Centric Approach to Federated System Identification: The FedAlign Framework

This paper presents FedAlign, a Federated Learning (FL) framework particularly designed for System Identification (SYSID) tasks by aligning state representations. Local workers can learn State-Space Models (SSMs) with equivalent representations but different dynamics. We demonstrate that directly aggregating these local SSMs via FedAvg results in a global model with altered system dynamics. FedAlign overcomes this problem by employing similarity transformation matrices to align state representations of local SSMs, thereby establishing a common parameter basin that retains the dynamics of local SSMs. FedAlign computes similarity transformation matrices via two distinct approaches: FedAlign-A and FedAlign-O. In FedAlign-A, we represent the global SSM in controllable canonical form (CCF). We apply control theory to analytically derive similarity transformation matrices that convert each local SSM into this form. Yet, establishing global SSM in CCF brings additional alignment challenges in multi input - multi output SYSID as CCF representation is not unique, unlike in single input - single output SYSID. In FedAlign-O, we address these alignment challenges by reformulating the local parameter basin alignment problem as an optimization task. We determine the parameter basin of a local worker as the common parameter basin and solve least square problems to obtain similarity transformation matrices needed to align the remaining local SSMs. Through the experiments conducted on synthetic and real-world datasets, we show that FedAlign outperforms FedAvg, converges faster, and provides improved stability of the global SSM thanks to the efficient alignment of local parameter basins.

Conformalized High-Density Quantile Regression via Dynamic Prototypes-based Probability Density Estimation

Recent methods in quantile regression have adopted a classification perspective to handle challenges posed by heteroscedastic, multimodal, or skewed data by quantizing outputs into fixed bins. Although these regression-as-classification frameworks can capture high-density prediction regions and bypass convex quantile constraints, they are restricted by quantization errors and the curse of dimensionality due to a constant number of bins per dimension. To address these limitations, we introduce a conformalized high-density quantile regression approach with a dynamically adaptive set of prototypes. Our method optimizes the set of prototypes by adaptively adding, deleting, and relocating quantization bins throughout the training process. Moreover, our conformal scheme provides valid coverage guarantees, focusing on regions with the highest probability density. Experiments across diverse datasets and dimensionalities confirm that our method consistently achieves high-quality prediction regions with enhanced coverage and robustness, all while utilizing fewer prototypes and memory, ensuring scalability to higher dimensions. The code is available at https://github.com/batuceng/max_quantile .

Efficient Learning of Fuzzy Logic Systems for Large-Scale Data Using Deep Learning

Type-1 and Interval Type-2 (IT2) Fuzzy Logic Systems (FLS) excel in handling uncertainty alongside their parsimonious rule-based structure. Yet, in learning large-scale data challenges arise, such as the curse of dimensionality and training complexity of FLSs. The complexity is due mainly to the constraints to be satisfied as the learnable parameters define FSs and the complexity of the center of the sets calculation method, especially of IT2-FLSs. This paper explicitly focuses on the learning problem of FLSs and presents a computationally efficient learning method embedded within the realm of Deep Learning (DL). The proposed method tackles the learning challenges of FLSs by presenting computationally efficient implementations of FLSs, thereby minimizing training time while leveraging mini-batched DL optimizers and automatic differentiation provided within the DL frameworks. We illustrate the efficiency of the DL framework for FLSs on benchmark datasets.