Fixed Point Iterations for SURE-based PSF Estimation for Image Deconvolution

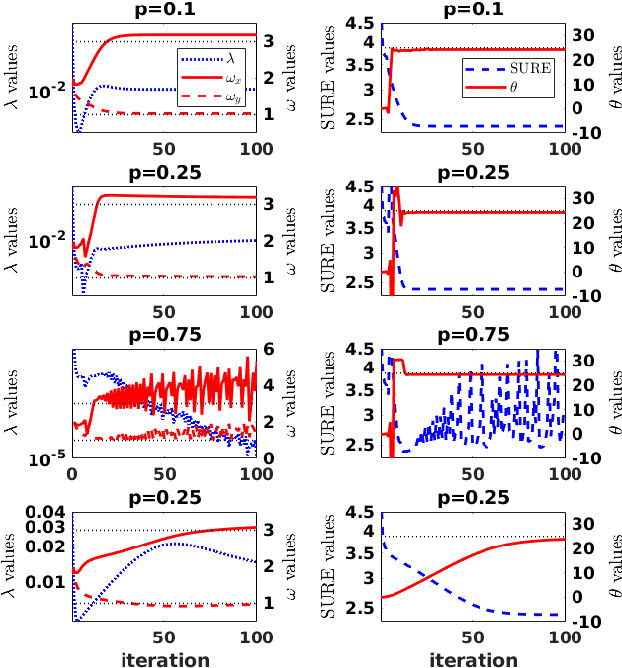
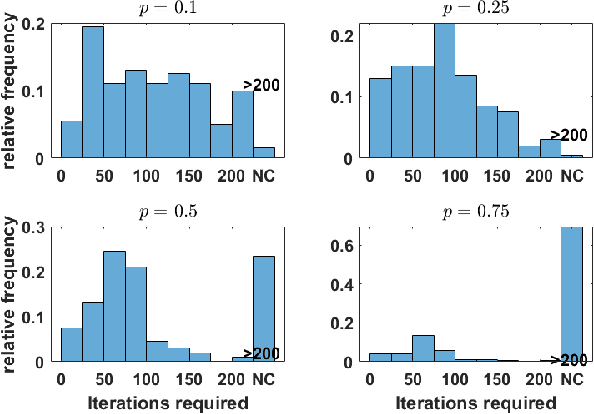
Stein's unbiased risk estimator (SURE) has been shown to be an effective metric for determining optimal parameters for many applications. The topic of this article is focused on the use of SURE for determining parameters for blind deconvolution. The parameters include those that define the shape of the point spread function (PSF), as well as regularization parameters in the deconvolution formulas. Within this context, the optimal parameters are typically determined via a brute for search over the feasible parameter space. When multiple parameters are involved, this parameter search is prohibitively costly due to the curse of dimensionality. In this work, novel fixed point iterations are proposed for optimizing these parameters, which allows for rapid estimation of a relatively large number of parameters. We demonstrate that with some mild tuning of the optimization parameters, these fixed point methods typically converge to the ideal PSF parameters in relatively few iterations, e.g. 50-100, with each iteration requiring very low computational cost.

New Computational Techniques for a Faster Variation of BM3D Image Denoising

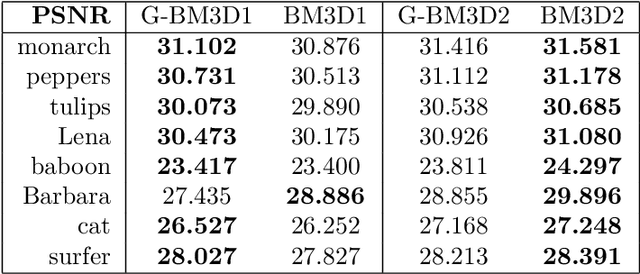
BM3D has been considered the standard for comparison in the image denoising literature for the last decade. Though it has been shown to be surpassed numerous times by alternative algorithms in terms of PSNR, the margins are very thin, and denoising is approaching a limiting point. The reason for the continued use of BM3D within the literature is due to its off-the-shelf ease-of-use in any application, which alternative improved denoising algorithms sometimes fail to match. This article proposes a new variation of BM3D, which maintains its ease of use but is notably faster. This development brings us closer to real-time ease-of-use application of new state-of-the-art image reconstruction algorithms such as plug-and-play priors. We refer to our variation of BM3D as G-BM3D. In terms of image quality, our algorithm attains very similar denoising performance to the original algorithm. Though our algorithm is written completely in MATLAB software, it is already between 5-20 times faster than the original algorithm, and the modifications to the algorithm are such that it is expected to be significantly faster when ported to CUDA language and with more powerful GPUs. The improved processing time is achieved by two main components. The first component is a new computational strategy that achieves faster block matching, and the second is a new global approach to the 3D wavelet filtering step that allows for significantly improved processing times on GPUs. The fast block matching strategy could also be applied to any of the vast number of nonlocal self-similarity (NSS) denoisers to improve processing times.