MixFunn: A Neural Network for Differential Equations with Improved Generalization and Interpretability

We introduce MixFunn, a novel neural network architecture designed to solve differential equations with enhanced precision, interpretability, and generalization capability. The architecture comprises two key components: the mixed-function neuron, which integrates multiple parameterized nonlinear functions to improve representational flexibility, and the second-order neuron, which combines a linear transformation of its inputs with a quadratic term to capture cross-combinations of input variables. These features significantly enhance the expressive power of the network, enabling it to achieve comparable or superior results with drastically fewer parameters and a reduction of up to four orders of magnitude compared to conventional approaches. We applied MixFunn in a physics-informed setting to solve differential equations in classical mechanics, quantum mechanics, and fluid dynamics, demonstrating its effectiveness in achieving higher accuracy and improved generalization to regions outside the training domain relative to standard machine learning models. Furthermore, the architecture facilitates the extraction of interpretable analytical expressions, offering valuable insights into the underlying solutions.

QuForge: A Library for Qudits Simulation

Quantum computing with qudits, an extension of qubits to multiple levels, is a research field less mature than qubit-based quantum computing. However, qudits can offer some advantages over qubits, by representing information with fewer separated components. In this article, we present QuForge, a Python-based library designed to simulate quantum circuits with qudits. This library provides the necessary quantum gates for implementing quantum algorithms, tailored to any chosen qudit dimension. Built on top of differentiable frameworks, QuForge supports execution on accelerating devices such as GPUs and TPUs, significantly speeding up simulations. It also supports sparse operations, leading to a reduction in memory consumption compared to other libraries. Additionally, by constructing quantum circuits as differentiable graphs, QuForge facilitates the implementation of quantum machine learning algorithms, enhancing the capabilities and flexibility of quantum computing research.

Barren plateaus induced by the dimension of qudits

Variational Quantum Algorithms (VQAs) have emerged as pivotal strategies for attaining quantum advantages in diverse scientific and technological domains, notably within Quantum Neural Networks. However, despite their potential, VQAs encounter significant obstacles, chief among them being the gradient vanishing problem, commonly referred to as barren plateaus. In this study, we unveil a direct correlation between the dimension of qudits and the occurrence of barren plateaus, a connection previously overlooked. Through meticulous analysis, we demonstrate that existing literature implicitly suggests the intrinsic influence of qudit dimensionality on barren plateaus. To instantiate these findings, we present numerical results that exemplify the impact of qudit dimensionality on barren plateaus. Additionally, despite the proposition of various error mitigation techniques, our results call for further scrutiny about their efficacy in the context of VQAs with qudits.

A differentiable programming framework for spin models

Spin systems are a powerful tool for modeling a wide range of physical systems. In this paper, we propose a novel framework for modeling spin systems using differentiable programming. Our approach enables us to efficiently simulate spin systems, making it possible to model complex systems at scale. Specifically, we demonstrate the effectiveness of our technique by applying it to three different spin systems: the Ising model, the Potts model, and the Cellular Potts model. Our simulations show that our framework offers significant speedup compared to traditional simulation methods, thanks to its ability to execute code efficiently across different hardware architectures, including Graphical Processing Units and Tensor Processing Units.

Feature Alignment for Approximated Reversibility in Neural Networks

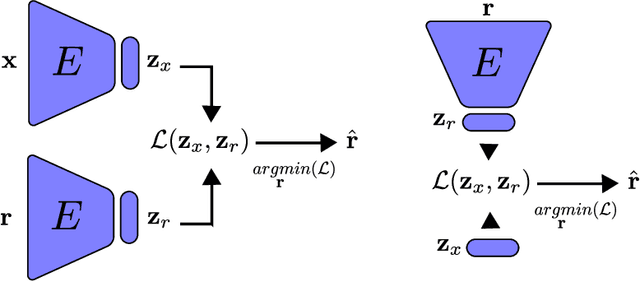
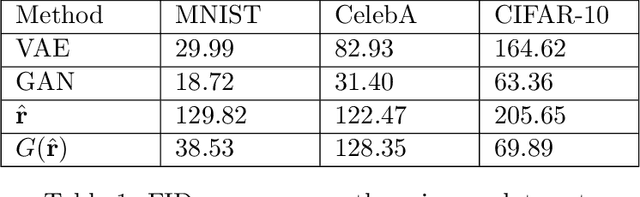
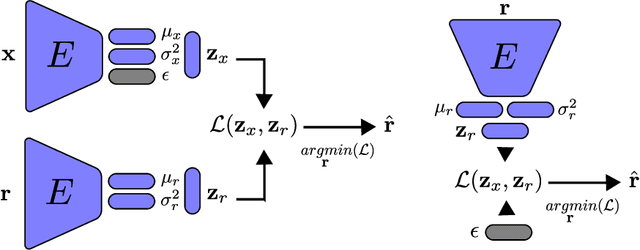
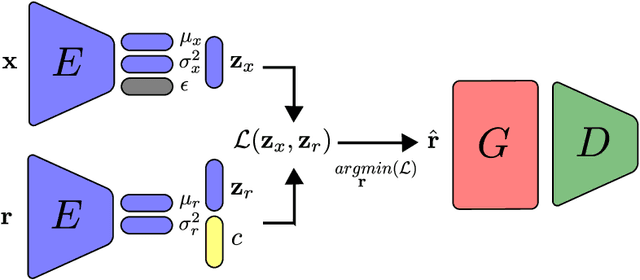
We introduce feature alignment, a technique for obtaining approximate reversibility in artificial neural networks. By means of feature extraction, we can train a neural network to learn an estimated map for its reverse process from outputs to inputs. Combined with variational autoencoders, we can generate new samples from the same statistics as the training data. Improvements of the results are obtained by using concepts from generative adversarial networks. Finally, we show that the technique can be modified for training neural networks locally, saving computational memory resources. Applying these techniques, we report results for three vision generative tasks: MNIST, CIFAR-10, and celebA.

Gradient target propagation

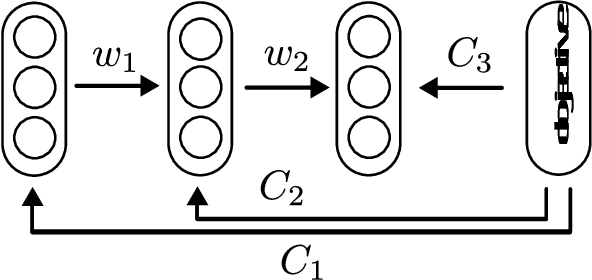
We report a learning rule for neural networks that computes how much each neuron should contribute to minimize a giving cost function via the estimation of its target value. By theoretical analysis, we show that this learning rule contains backpropagation, Hebian learning, and additional terms. We also give a general technique for weights initialization. Our results are at least as good as those obtained with backpropagation. The neural networks are trained and tested in three problems: MNIST, MNIST-Fashion, and CIFAR-10 datasets. The associated code is available at https://github.com/tiago939/target.