A Gauss-Newton Method for Markov Decision Processes

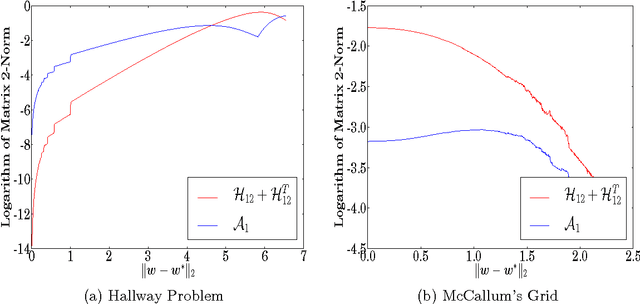
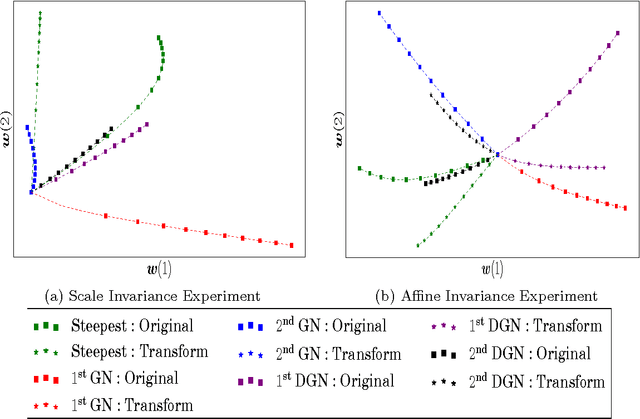
Approximate Newton methods are a standard optimization tool which aim to maintain the benefits of Newton's method, such as a fast rate of convergence, whilst alleviating its drawbacks, such as computationally expensive calculation or estimation of the inverse Hessian. In this work we investigate approximate Newton methods for policy optimization in Markov Decision Processes (MDPs). We first analyse the structure of the Hessian of the objective function for MDPs. We show that, like the gradient, the Hessian exhibits useful structure in the context of MDPs and we use this analysis to motivate two Gauss-Newton Methods for MDPs. Like the Gauss-Newton method for non-linear least squares, these methods involve approximating the Hessian by ignoring certain terms in the Hessian which are difficult to estimate. The approximate Hessians possess desirable properties, such as negative definiteness, and we demonstrate several important performance guarantees including guaranteed ascent directions, invariance to affine transformation of the parameter space, and convergence guarantees. We finally provide a unifying perspective of key policy search algorithms, demonstrating that our second Gauss-Newton algorithm is closely related to both the EM-algorithm and natural gradient ascent applied to MDPs, but performs significantly better in practice on a range of challenging domains.

Efficient Inference in Markov Control Problems

Markov control algorithms that perform smooth, non-greedy updates of the policy have been shown to be very general and versatile, with policy gradient and Expectation Maximisation algorithms being particularly popular. For these algorithms, marginal inference of the reward weighted trajectory distribution is required to perform policy updates. We discuss a new exact inference algorithm for these marginals in the finite horizon case that is more efficient than the standard approach based on classical forward-backward recursions. We also provide a principled extension to infinite horizon Markov Decision Problems that explicitly accounts for an infinite horizon. This extension provides a novel algorithm for both policy gradients and Expectation Maximisation in infinite horizon problems.