An Elementary Proof of the Near Optimality of LogSumExp Smoothing

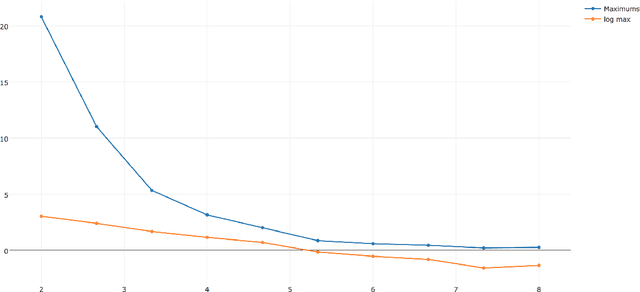
We consider the design of smoothings of the (coordinate-wise) max function in $\mathbb{R}^d$ in the infinity norm. The LogSumExp function $f(x)=\ln(\sum^d_i\exp(x_i))$ provides a classical smoothing, differing from the max function in value by at most $\ln(d)$. We provide an elementary construction of a lower bound, establishing that every overestimating smoothing of the max function must differ by at least $\sim 0.8145\ln(d)$. Hence, LogSumExp is optimal up to constant factors. However, in small dimensions, we provide stronger, exactly optimal smoothings attaining our lower bound, showing that the entropy-based LogSumExp approach to smoothing is not exactly optimal.

On the Consistency of Graph-based Bayesian Learning and the Scalability of Sampling Algorithms

A popular approach to semi-supervised learning proceeds by endowing the input data with a graph structure in order to extract geometric information and incorporate it into a Bayesian framework. We introduce new theory that gives appropriate scalings of graph parameters that provably lead to a well-defined limiting posterior as the size of the unlabeled data set grows. Furthermore, we show that these consistency results have profound algorithmic implications. When consistency holds, carefully designed graph-based Markov chain Monte Carlo algorithms are proved to have a uniform spectral gap, independent of the number of unlabeled inputs. Several numerical experiments corroborate both the statistical consistency and the algorithmic scalability established by the theory.