Efficient Bayesian Computation Using Plug-and-Play Priors for Poisson Inverse Problems

This paper introduces a novel plug-and-play (PnP) Langevin sampling methodology for Bayesian inference in low-photon Poisson imaging problems, a challenging class of problems with significant applications in astronomy, medicine, and biology. PnP Langevin sampling algorithms offer a powerful framework for Bayesian image restoration, enabling accurate point estimation as well as advanced inference tasks, including uncertainty quantification and visualization analyses, and empirical Bayesian inference for automatic model parameter tuning. However, existing PnP Langevin algorithms are not well-suited for low-photon Poisson imaging due to high solution uncertainty and poor regularity properties, such as exploding gradients and non-negativity constraints. To address these challenges, we propose two strategies for extending Langevin PnP sampling to Poisson imaging models: (i) an accelerated PnP Langevin method that incorporates boundary reflections and a Poisson likelihood approximation and (ii) a mirror sampling algorithm that leverages a Riemannian geometry to handle the constraints and the poor regularity of the likelihood without approximations. The effectiveness of these approaches is demonstrated through extensive numerical experiments and comparisons with state-of-the-art methods.

Accelerated Bayesian imaging by relaxed proximal-point Langevin sampling

This paper presents a new accelerated proximal Markov chain Monte Carlo methodology to perform Bayesian inference in imaging inverse problems with an underlying convex geometry. The proposed strategy takes the form of a stochastic relaxed proximal-point iteration that admits two complementary interpretations. For models that are smooth or regularised by Moreau-Yosida smoothing, the algorithm is equivalent to an implicit midpoint discretisation of an overdamped Langevin diffusion targeting the posterior distribution of interest. This discretisation is asymptotically unbiased for Gaussian targets and shown to converge in an accelerated manner for any target that is $\kappa$-strongly log-concave (i.e., requiring in the order of $\sqrt{\kappa}$ iterations to converge, similarly to accelerated optimisation schemes), comparing favorably to [M. Pereyra, L. Vargas Mieles, K.C. Zygalakis, SIAM J. Imaging Sciences, 13, 2 (2020), pp. 905-935] which is only provably accelerated for Gaussian targets and has bias. For models that are not smooth, the algorithm is equivalent to a Leimkuhler-Matthews discretisation of a Langevin diffusion targeting a Moreau-Yosida approximation of the posterior distribution of interest, and hence achieves a significantly lower bias than conventional unadjusted Langevin strategies based on the Euler-Maruyama discretisation. For targets that are $\kappa$-strongly log-concave, the provided non-asymptotic convergence analysis also identifies the optimal time step which maximizes the convergence speed. The proposed methodology is demonstrated through a range of experiments related to image deconvolution with Gaussian and Poisson noise, with assumption-driven and data-driven convex priors.

Learning a Variational Network for Reconstruction of Accelerated MRI Data

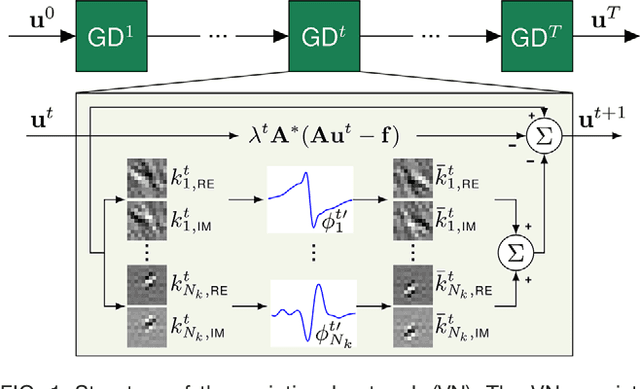
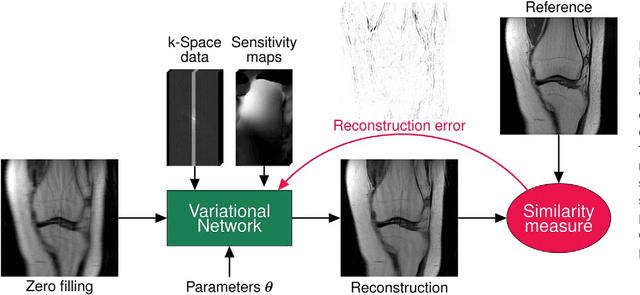
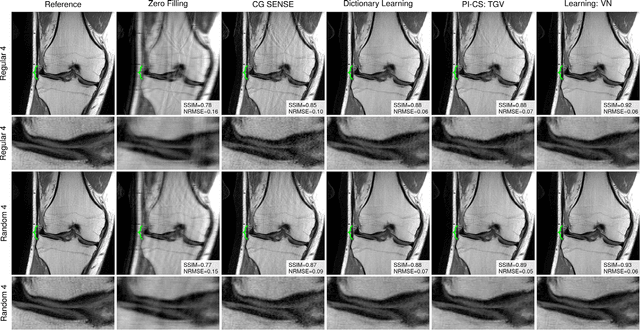
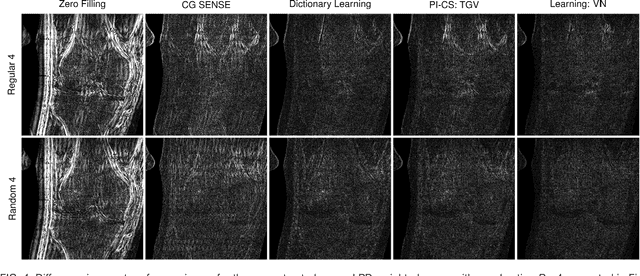
Purpose: To allow fast and high-quality reconstruction of clinical accelerated multi-coil MR data by learning a variational network that combines the mathematical structure of variational models with deep learning. Theory and Methods: Generalized compressed sensing reconstruction formulated as a variational model is embedded in an unrolled gradient descent scheme. All parameters of this formulation, including the prior model defined by filter kernels and activation functions as well as the data term weights, are learned during an offline training procedure. The learned model can then be applied online to previously unseen data. Results: The variational network approach is evaluated on a clinical knee imaging protocol. The variational network reconstructions outperform standard reconstruction algorithms in terms of image quality and residual artifacts for all tested acceleration factors and sampling patterns. Conclusion: Variational network reconstructions preserve the natural appearance of MR images as well as pathologies that were not included in the training data set. Due to its high computational performance, i.e., reconstruction time of 193 ms on a single graphics card, and the omission of parameter tuning once the network is trained, this new approach to image reconstruction can easily be integrated into clinical workflow.