Explorative Curriculum Learning for Strongly Correlated Electron Systems

Recent advances in neural network quantum states (NQS) have enabled high-accuracy predictions for complex quantum many-body systems such as strongly correlated electron systems. However, the computational cost remains prohibitive, making exploration of the diverse parameters of interaction strengths and other physical parameters inefficient. While transfer learning has been proposed to mitigate this challenge, achieving generalization to large-scale systems and diverse parameter regimes remains difficult. To address this limitation, we propose a novel curriculum learning framework based on transfer learning for NQS. This facilitates efficient and stable exploration across a vast parameter space of quantum many-body systems. In addition, by interpreting NQS transfer learning through a perturbative lens, we demonstrate how prior physical knowledge can be flexibly incorporated into the curriculum learning process. We also propose Pairing-Net, an architecture to practically implement this strategy for strongly correlated electron systems, and empirically verify its effectiveness. Our results show an approximately 200-fold speedup in computation and a marked improvement in optimization stability compared to conventional methods.

Stable Invariant Models via Koopman Spectra

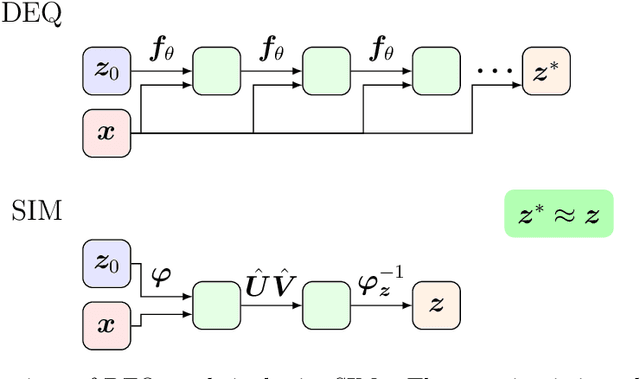
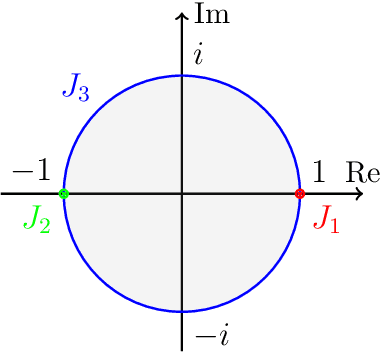
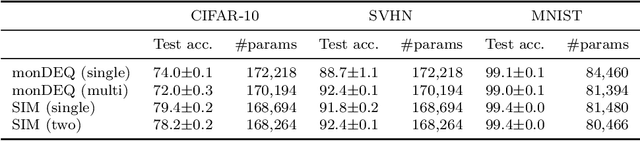
Weight-tied models have attracted attention in the modern development of neural networks. The deep equilibrium model (DEQ) represents infinitely deep neural networks with weight-tying, and recent studies have shown the potential of this type of approach. DEQs are needed to iteratively solve root-finding problems in training and are built on the assumption that the underlying dynamics determined by the models converge to a fixed point. In this paper, we present the stable invariant model (SIM), a new class of deep models that in principle approximates DEQs under stability and extends the dynamics to more general ones converging to an invariant set (not restricted in a fixed point). The key ingredient in deriving SIMs is a representation of the dynamics with the spectra of the Koopman and Perron--Frobenius operators. This perspective approximately reveals stable dynamics with DEQs and then derives two variants of SIMs. We also propose an implementation of SIMs that can be learned in the same way as feedforward models. We illustrate the empirical performance of SIMs with experiments and demonstrate that SIMs achieve comparative or superior performance against DEQs in several learning tasks.

A Tractable Fully Bayesian Method for the Stochastic Block Model

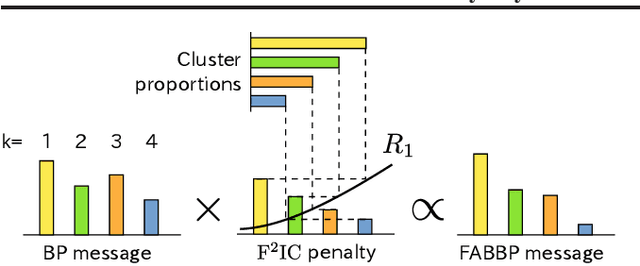
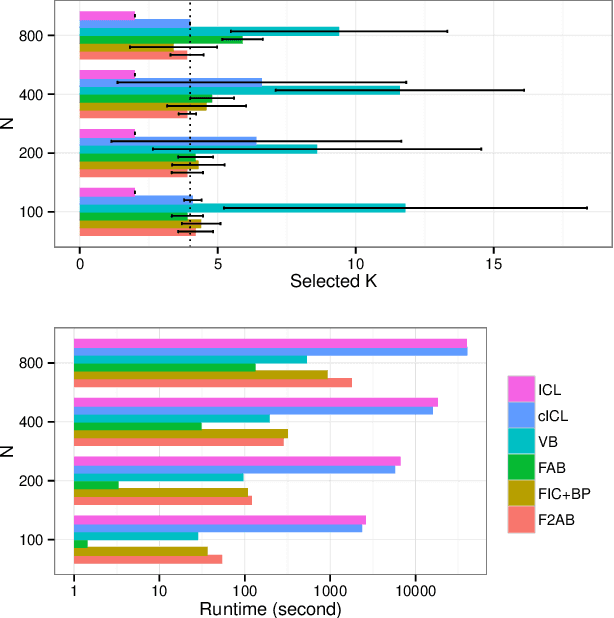
The stochastic block model (SBM) is a generative model revealing macroscopic structures in graphs. Bayesian methods are used for (i) cluster assignment inference and (ii) model selection for the number of clusters. In this paper, we study the behavior of Bayesian inference in the SBM in the large sample limit. Combining variational approximation and Laplace's method, a consistent criterion of the fully marginalized log-likelihood is established. Based on that, we derive a tractable algorithm that solves tasks (i) and (ii) concurrently, obviating the need for an outer loop to check all model candidates. Our empirical and theoretical results demonstrate that our method is scalable in computation, accurate in approximation, and concise in model selection.