Internalized Morphogenesis: A Self-Organizing Model for Growth, Replication, and Regeneration via Local Token Exchange in Modular Systems

This study presents an internalized morphogenesis model for autonomous systems, such as swarm robotics and micro-nanomachines, that eliminates the need for external spatial computation. Traditional self-organizing models often require calculations across the entire coordinate space, including empty areas, which is impractical for resource-constrained physical modules. Our proposed model achieves complex morphogenesis through strictly local interactions between adjacent modules within the "body." By extending the "Ishida token model," modules exchange integer values using an RD-inspired discrete analogue without solving differential equations. The internal potential, derived from token accumulation and aging, guides autonomous growth, shrinkage, and replication. Simulations on a hexagonal grid demonstrated the emergence of limb-like extensions, self-division, and robust regeneration capabilities following structural amputation. A key feature is the use of the body boundary as a natural sink for information entropy (tokens) to maintain a dynamic equilibrium. These results indicate that sophisticated morphological behaviors can emerge from minimal, internal-only rules. This framework offers a computationally efficient and biologically plausible approach to developing self-repairing, adaptive, and autonomous hardware.

An algorithm applied the Turing pattern model to control active swarm robots using only information from neighboring modules

Swarm robots, inspired by the emergence of animal herds, are robots that assemble a large number of modules and self-organize themselves to form specific morphologies and exhibit specific functions. These modular robots perform relatively simple actions and controls, and create macroscopic morphologies and functions through the interaction of a large number of modular robots. This research focuses on such self-organizing robots or swarm robots. The proposed algorithm is a model that applies the Turing pattern, one of the self-organization models, to make a group of modules accumulate and stay within a certain region. The proposed method utilizes the area within the spots of the Turing pattern as the aggregation region of the modules. Furthermore, it considers the value corresponding to the concentration distribution within the spotted pattern of the Turing pattern model (referred to as the potential value in this research), identifies the center of the region (spotted pattern), and makes it the center of the module group. By controlling the modules in the direction of the higher potential value, it succeeds in maintaining the shape of the module group as a whole while moving. The algorithm was validated using a two-dimensional simulation model. The unit module robot was assumed to have the following properties: 1) limited self-drive, 2) no module identifier, 3) information exchange only with adjacent modules, 4) no coordinate system, and 5) only simple arithmetic and memory functions. Using these modules, the devised algorithm was able to achieve not only the creation of static forms but also the realization of the following movements: 1) modules accumulate and grow, 2) modules move to the light source, 3) exit the gap while maintaining its shape, and 4) self-replication.

Mimicry mechanism model of octopus epidermis pattern by inverse operation of Turing reaction model

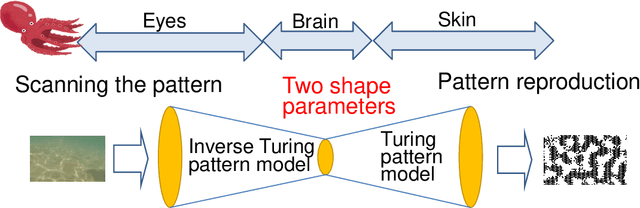
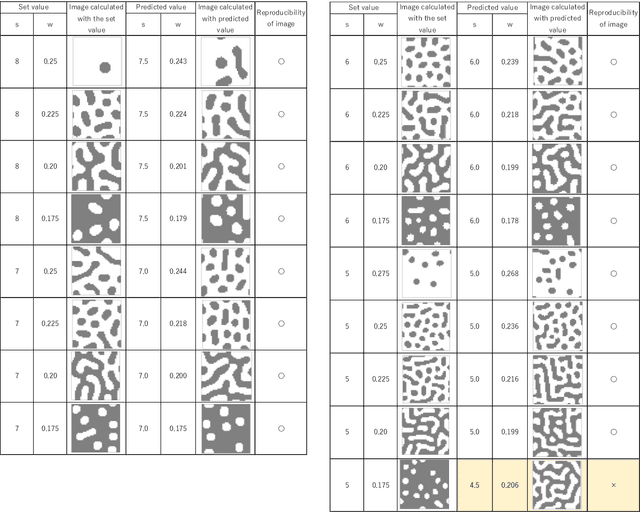
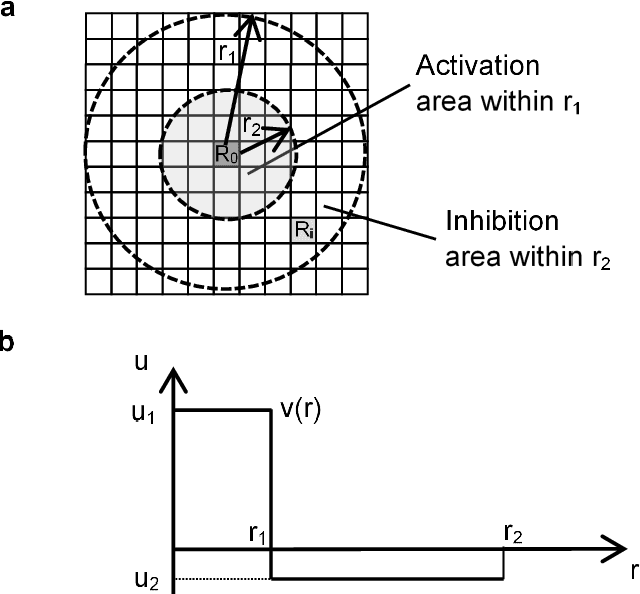
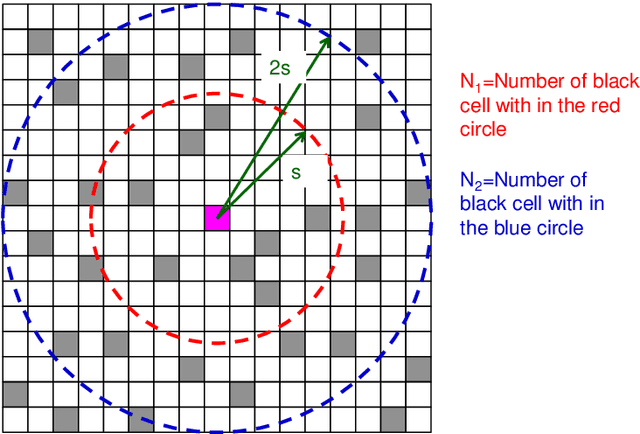
Many cephalopods such as octopus and squid change their skin color purposefully within a very short time. Furthermore, it is widely known that some octopuses have the ability to change the color and unevenness of the skin and to mimic the surroundings in short time. However, much research has not been done on the entire mimicry mechanism in which the octopus recognizes the surrounding landscape and changes the skin pattern. It seems that there is no hypothetical model to explain the whole mimicry mechanism yet. In this study, the mechanism of octopus skin pattern formation was assumed to be based on the Turing model. Here, the pattern formation by the Turing model was realized by the equivalent filter calculation model using the cellular automaton, instead of directly solving the differential equations. It was shown that this model can create various patterns with two feature parameters. Furthermore, for the eyes recognition part where two features are extracted from the Turing pattern image, our study proposed a method that can be calculated back with small amount of calculation using the characteristics of the cellular Turing pattern model. These two calculations can be expressed in the same mathematical frame based on the cellular automaton model using the convolution filter. As a result, it can be created a model which is capable of extracting features from patterns and reconstructing patterns in a short time, the model is considered to be a basic model for considering the mimicry mechanism of octopus. Also, in terms of application to machine learning, it is considered that it shows the possibility of leading to a model with a small amount of learning calculation.