On the Boolean Network Theory of Datalog$^ eg$

Datalog$^\neg$ is a central formalism used in a variety of domains ranging from deductive databases and abstract argumentation frameworks to answer set programming. Its model theory is the finite counterpart of the logical semantics developed for normal logic programs, mainly based on the notions of Clark's completion and two-valued or three-valued canonical models including supported, stable, regular and well-founded models. In this paper we establish a formal link between Datalog$^\neg$ and Boolean network theory, which was initially introduced by Stuart Kaufman and Ren\'e Thomas to reason about gene regulatory networks. We use previous results from Boolean network theory to prove that in the absence of odd cycles in a Datalog$^\neg$ program, the regular models coincide with the stable models, which entails the existence of stable models, and in the absence of even cycles, we show the uniqueness of stable partial models, which entails the uniqueness of regular models. These results on regular models have been claimed by You and Yuan in 1994 for normal logic programs but we show problems in their definition of well-founded stratification and in their proofs that we can fix for negative normal logic programs only. We also give upper bounds on the numbers of stable partial, regular, and stable models of a Datalog$^\neg$ program using the cardinality of a feedback vertex set in its atom dependency graph. Interestingly, our connection to Boolean network theory also points us to the notion of trap spaces for Datalog$^\neg$ programs. We relate the notions of supported or stable trap spaces to the other semantics of Datalog$^\neg$, and show the equivalence between subset-minimal stable trap spaces and regular models.

Graphical Conditions for the Existence, Unicity and Number of Regular Models

The regular models of a normal logic program are a particular type of partial (i.e. 3-valued) models which correspond to stable partial models with minimal undefinedness. In this paper, we explore graphical conditions on the dependency graph of a finite ground normal logic program to analyze the existence, unicity and number of regular models for the program. We show three main results: 1) a necessary condition for the existence of non-trivial (i.e. non-2-valued) regular models, 2) a sufficient condition for the unicity of regular models, and 3) two upper bounds for the number of regular models based on positive feedback vertex sets. The first two conditions generalize the finite cases of the two existing results obtained by You and Yuan (1994) for normal logic programs with well-founded stratification. The third result is also new to the best of our knowledge. Key to our proofs is a connection that we establish between finite ground normal logic programs and Boolean network theory.

Reactmine: a search algorithm for inferring chemical reaction networks from time series data

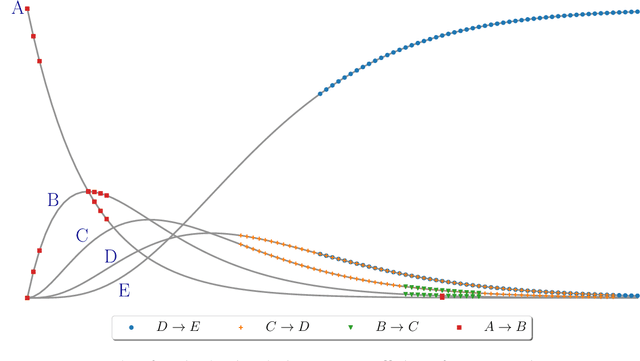
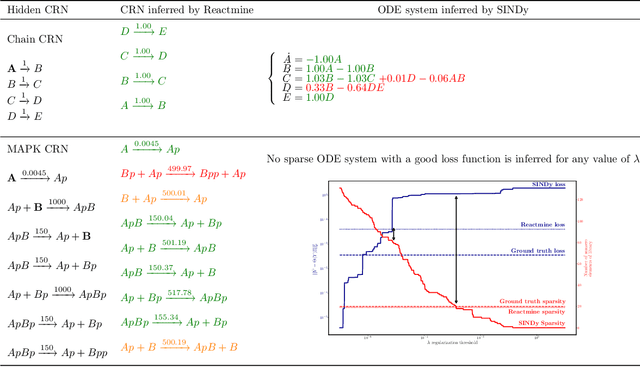
Inferring chemical reaction networks (CRN) from time series data is a challenge encouraged by the growing availability of quantitative temporal data at the cellular level. This motivates the design of algorithms to infer the preponderant reactions between the molecular species observed in a given biochemical process, and help to build CRN model structure and kinetics. Existing ODE-based inference methods such as SINDy resort to least square regression combined with sparsity-enforcing penalization, such as Lasso. However, when the input time series are only available in wild type conditions in which all reactions are present, we observe that current methods fail to learn sparse models. Results: We present Reactmine, a CRN learning algorithm which enforces sparsity by inferring reactions in a sequential fashion within a search tree of bounded depth, ranking the inferred reaction candidates according to the variance of their kinetics, and re-optimizing the CRN kinetic parameters on the whole trace in a final pass to rank the inferred CRN candidates. We first evaluate its performance on simulation data from a benchmark of hidden CRNs, together with algorithmic hyperparameter sensitivity analyses, and then on two sets of real experimental data: one from protein fluorescence videomicroscopy of cell cycle and circadian clock markers, and one from biomedical measurements of systemic circadian biomarkers possibly acting on clock gene expression in peripheral organs. We show that Reactmine succeeds both on simulation data by retrieving hidden CRNs where SINDy fails, and on the two real datasets by inferring reactions in agreement with previous studies.