Sylvain Gelly
INRIA Futurs
AdaGAN: Boosting Generative Models
May 24, 2017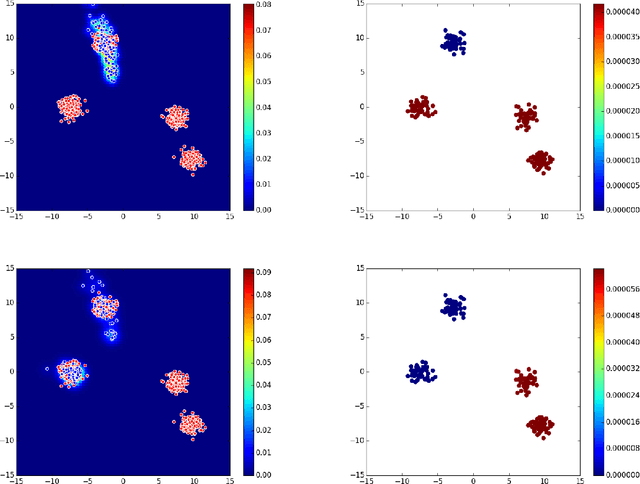
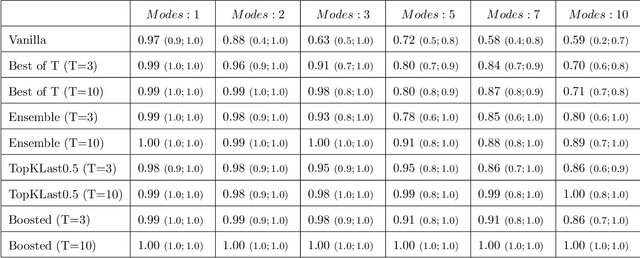
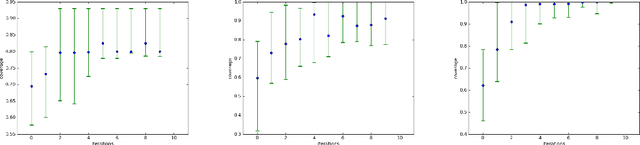
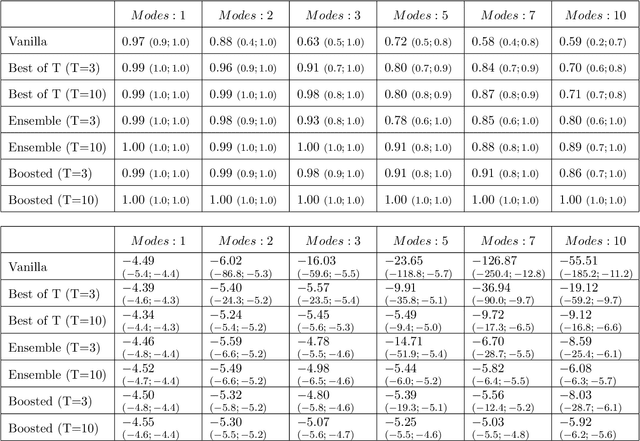
Abstract:Generative Adversarial Networks (GAN) (Goodfellow et al., 2014) are an effective method for training generative models of complex data such as natural images. However, they are notoriously hard to train and can suffer from the problem of missing modes where the model is not able to produce examples in certain regions of the space. We propose an iterative procedure, called AdaGAN, where at every step we add a new component into a mixture model by running a GAN algorithm on a reweighted sample. This is inspired by boosting algorithms, where many potentially weak individual predictors are greedily aggregated to form a strong composite predictor. We prove that such an incremental procedure leads to convergence to the true distribution in a finite number of steps if each step is optimal, and convergence at an exponential rate otherwise. We also illustrate experimentally that this procedure addresses the problem of missing modes.
From optimal transport to generative modeling: the VEGAN cookbook
May 22, 2017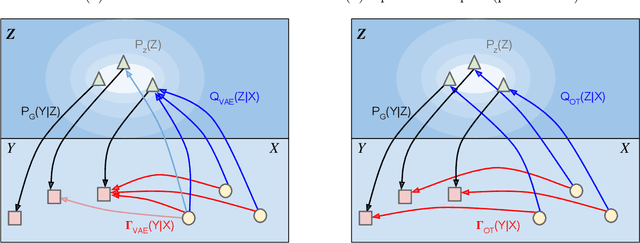
Abstract:We study unsupervised generative modeling in terms of the optimal transport (OT) problem between true (but unknown) data distribution $P_X$ and the latent variable model distribution $P_G$. We show that the OT problem can be equivalently written in terms of probabilistic encoders, which are constrained to match the posterior and prior distributions over the latent space. When relaxed, this constrained optimization problem leads to a penalized optimal transport (POT) objective, which can be efficiently minimized using stochastic gradient descent by sampling from $P_X$ and $P_G$. We show that POT for the 2-Wasserstein distance coincides with the objective heuristically employed in adversarial auto-encoders (AAE) (Makhzani et al., 2016), which provides the first theoretical justification for AAEs known to the authors. We also compare POT to other popular techniques like variational auto-encoders (VAE) (Kingma and Welling, 2014). Our theoretical results include (a) a better understanding of the commonly observed blurriness of images generated by VAEs, and (b) establishing duality between Wasserstein GAN (Arjovsky and Bottou, 2017) and POT for the 1-Wasserstein distance.
Artificial Agents and Speculative Bubbles
Nov 28, 2005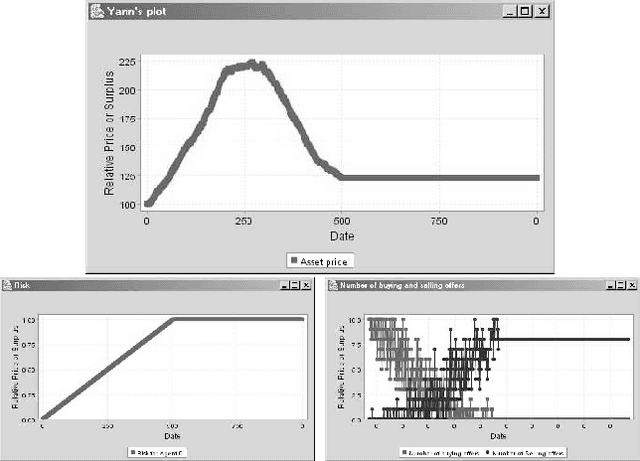
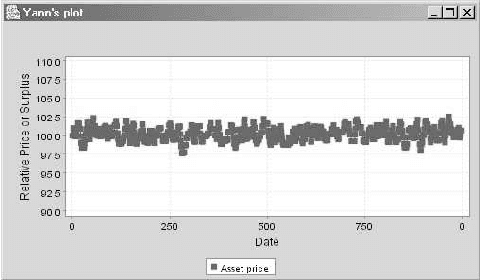
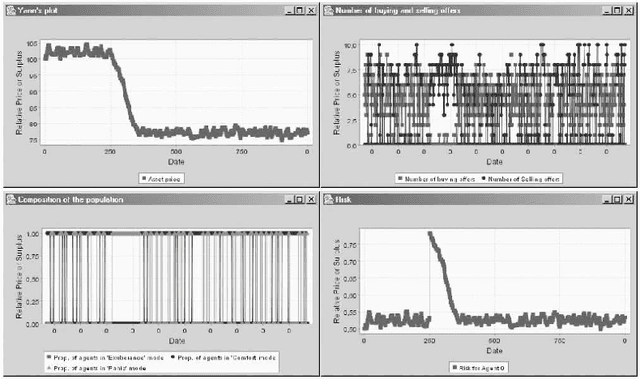
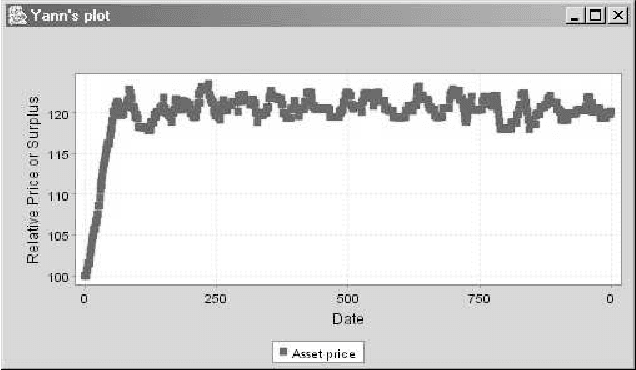
Abstract:Pertaining to Agent-based Computational Economics (ACE), this work presents two models for the rise and downfall of speculative bubbles through an exchange price fixing based on double auction mechanisms. The first model is based on a finite time horizon context, where the expected dividends decrease along time. The second model follows the {\em greater fool} hypothesis; the agent behaviour depends on the comparison of the estimated risk with the greater fool's. Simulations shed some light on the influent parameters and the necessary conditions for the apparition of speculative bubbles in an asset market within the considered framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge