Optimal Linear Combination of Classifiers

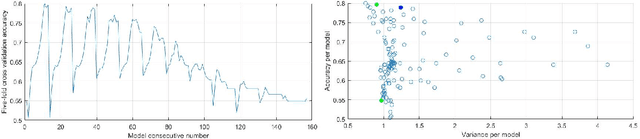
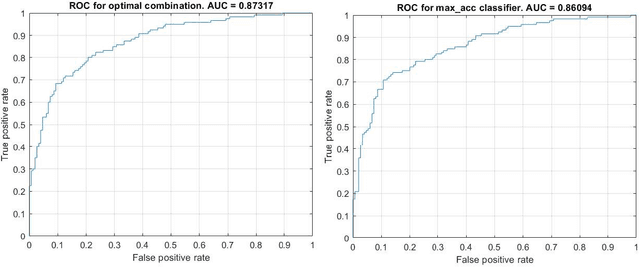
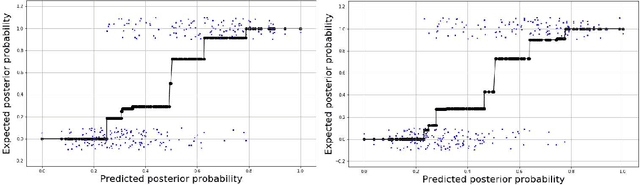
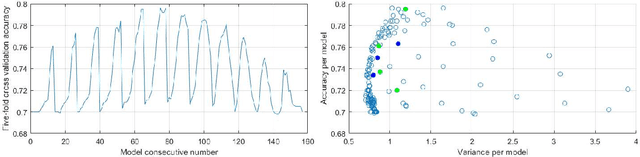
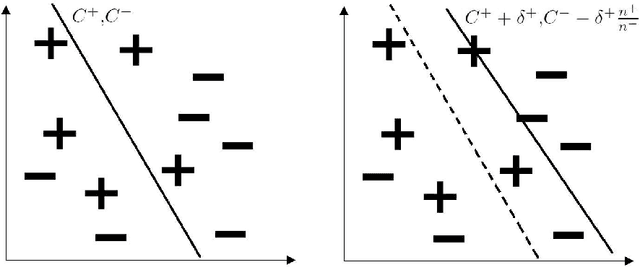
The question of whether to use one classifier or a combination of classifiers is a central topic in Machine Learning. We propose here a method for finding an optimal linear combination of classifiers derived from a bias-variance framework for the classification task.

Tutorial on Implied Posterior Probability for SVMs

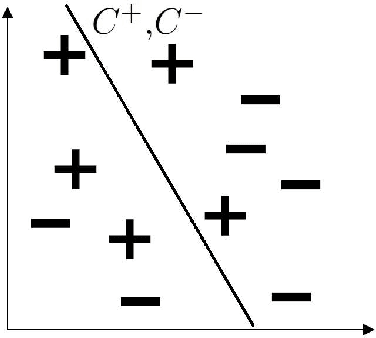
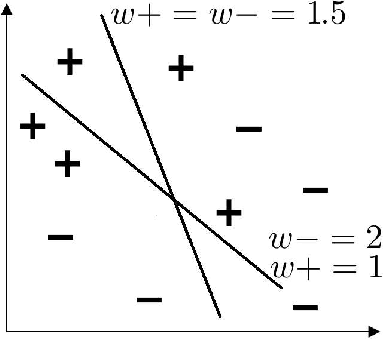
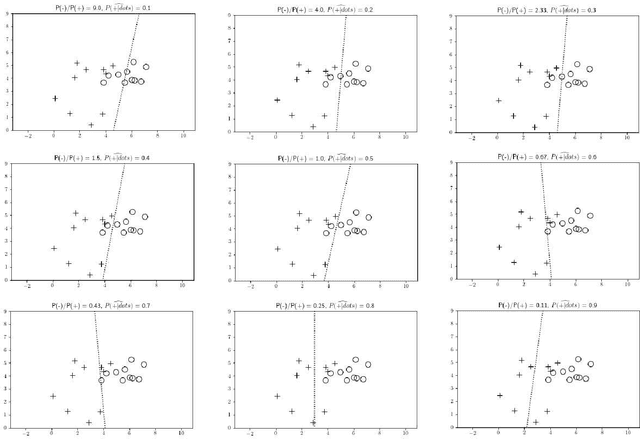
Implied posterior probability of a given model (say, Support Vector Machines (SVM)) at a point $\bf{x}$ is an estimate of the class posterior probability pertaining to the class of functions of the model applied to a given dataset. It can be regarded as a score (or estimate) for the true posterior probability, which can then be calibrated/mapped onto expected (non-implied by the model) posterior probability implied by the underlying functions, which have generated the data. In this tutorial we discuss how to compute implied posterior probabilities of SVMs for the binary classification case as well as how to calibrate them via a standard method of isotonic regression.

A Note on Posterior Probability Estimation for Classifiers

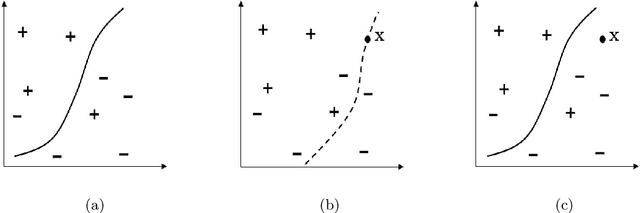
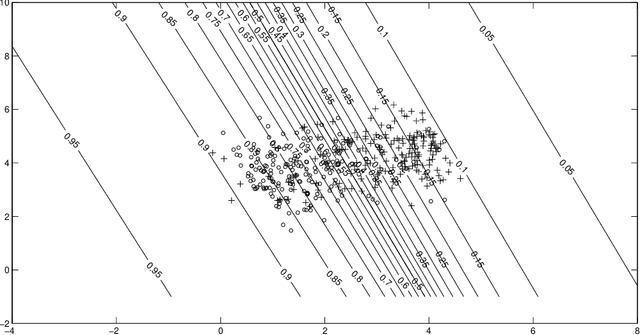
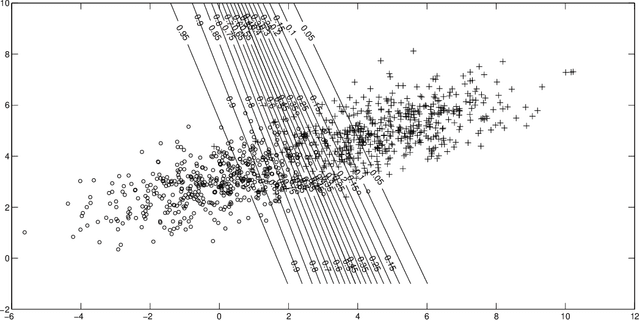
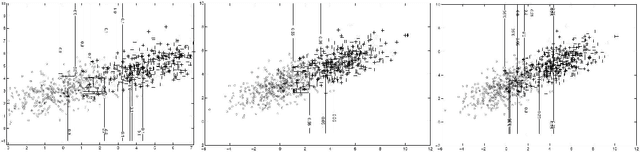
One of the central themes in the classification task is the estimation of class posterior probability at a new point $\bf{x}$. The vast majority of classifiers output a score for $\bf{x}$, which is monotonically related to the posterior probability via an unknown relationship. There are many attempts in the literature to estimate this latter relationship. Here, we provide a way to estimate the posterior probability without resorting to using classification scores. Instead, we vary the prior probabilities of classes in order to derive the ratio of pdf's at point $\bf{x}$, which is directly used to determine class posterior probabilities. We consider here the binary classification problem.