Near-Optimal Regret-Queue Length Tradeoff in Online Learning for Two-Sided Markets

We study a two-sided market, wherein, price-sensitive heterogeneous customers and servers arrive and join their respective queues. A compatible customer-server pair can then be matched by the platform, at which point, they leave the system. Our objective is to design pricing and matching algorithms that maximize the platform's profit, while maintaining reasonable queue lengths. As the demand and supply curves governing the price-dependent arrival rates may not be known in practice, we design a novel online-learning-based pricing policy and establish its near-optimality. In particular, we prove a tradeoff among three performance metrics: $\tilde{O}(T^{1-\gamma})$ regret, $\tilde{O}(T^{\gamma/2})$ average queue length, and $\tilde{O}(T^{\gamma})$ maximum queue length for $\gamma \in (0, 1/6]$, significantly improving over existing results [1]. Moreover, barring the permissible range of $\gamma$, we show that this trade-off between regret and average queue length is optimal up to logarithmic factors under a class of policies, matching the optimal one as in [2] which assumes the demand and supply curves to be known. Our proposed policy has two noteworthy features: a dynamic component that optimizes the tradeoff between low regret and small queue lengths; and a probabilistic component that resolves the tension between obtaining useful samples for fast learning and maintaining small queue lengths.

Graph Alignment via Birkhoff Relaxation

We consider the graph alignment problem, wherein the objective is to find a vertex correspondence between two graphs that maximizes the edge overlap. The graph alignment problem is an instance of the quadratic assignment problem (QAP), known to be NP-hard in the worst case even to approximately solve. In this paper, we analyze Birkhoff relaxation, a tight convex relaxation of QAP, and present theoretical guarantees on its performance when the inputs follow the Gaussian Wigner Model. More specifically, the weighted adjacency matrices are correlated Gaussian Orthogonal Ensemble with correlation $1/\sqrt{1+\sigma^2}$. Denote the optimal solutions of the QAP and Birkhoff relaxation by $\Pi^\star$ and $X^\star$ respectively. We show that $\|X^\star-\Pi^\star\|_F^2 = o(n)$ when $\sigma = o(n^{-1.25})$ and $\|X^\star-\Pi^\star\|_F^2 = \Omega(n)$ when $\sigma = \Omega(n^{-0.5})$. Thus, the optimal solution $X^\star$ transitions from a small perturbation of $\Pi^\star$ for small $\sigma$ to being well separated from $\Pi^\star$ as $\sigma$ becomes larger than $n^{-0.5}$. This result allows us to guarantee that simple rounding procedures on $X^\star$ align $1-o(1)$ fraction of vertices correctly whenever $\sigma = o(n^{-1.25})$. This condition on $\sigma$ to ensure the success of the Birkhoff relaxation is state-of-the-art.

On the Linear convergence of Natural Policy Gradient Algorithm

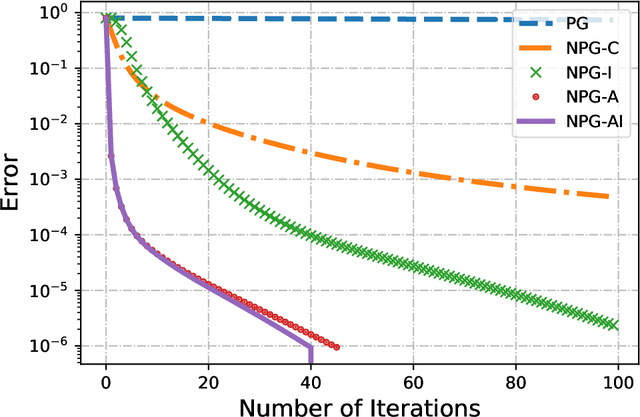
Markov Decision Processes are classically solved using Value Iteration and Policy Iteration algorithms. Recent interest in Reinforcement Learning has motivated the study of methods inspired by optimization, such as gradient ascent. Among these, a popular algorithm is the Natural Policy Gradient, which is a mirror descent variant for MDPs. This algorithm forms the basis of several popular Reinforcement Learning algorithms such as Natural actor-critic, TRPO, PPO, etc, and so is being studied with growing interest. It has been shown that Natural Policy Gradient with constant step size converges with a sublinear rate of O(1/k) to the global optimal. In this paper, we present improved finite time convergence bounds, and show that this algorithm has geometric (also known as linear) asymptotic convergence rate. We further improve this convergence result by introducing a variant of Natural Policy Gradient with adaptive step sizes. Finally, we compare different variants of policy gradient methods experimentally.