Continuum Dropout for Neural Differential Equations

Neural Differential Equations (NDEs) excel at modeling continuous-time dynamics, effectively handling challenges such as irregular observations, missing values, and noise. Despite their advantages, NDEs face a fundamental challenge in adopting dropout, a cornerstone of deep learning regularization, making them susceptible to overfitting. To address this research gap, we introduce Continuum Dropout, a universally applicable regularization technique for NDEs built upon the theory of alternating renewal processes. Continuum Dropout formulates the on-off mechanism of dropout as a stochastic process that alternates between active (evolution) and inactive (paused) states in continuous time. This provides a principled approach to prevent overfitting and enhance the generalization capabilities of NDEs. Moreover, Continuum Dropout offers a structured framework to quantify predictive uncertainty via Monte Carlo sampling at test time. Through extensive experiments, we demonstrate that Continuum Dropout outperforms existing regularization methods for NDEs, achieving superior performance on various time series and image classification tasks. It also yields better-calibrated and more trustworthy probability estimates, highlighting its effectiveness for uncertainty-aware modeling.

FlowPath: Learning Data-Driven Manifolds with Invertible Flows for Robust Irregularly-sampled Time Series Classification

Modeling continuous-time dynamics from sparse and irregularly-sampled time series remains a fundamental challenge. Neural controlled differential equations provide a principled framework for such tasks, yet their performance is highly sensitive to the choice of control path constructed from discrete observations. Existing methods commonly employ fixed interpolation schemes, which impose simplistic geometric assumptions that often misrepresent the underlying data manifold, particularly under high missingness. We propose FlowPath, a novel approach that learns the geometry of the control path via an invertible neural flow. Rather than merely connecting observations, FlowPath constructs a continuous and data-adaptive manifold, guided by invertibility constraints that enforce information-preserving and well-behaved transformations. This inductive bias distinguishes FlowPath from prior unconstrained learnable path models. Empirical evaluations on 18 benchmark datasets and a real-world case study demonstrate that FlowPath consistently achieves statistically significant improvements in classification accuracy over baselines using fixed interpolants or non-invertible architectures. These results highlight the importance of modeling not only the dynamics along the path but also the geometry of the path itself, offering a robust and generalizable solution for learning from irregular time series.

Modeling Irregular Astronomical Time Series with Neural Stochastic Delay Differential Equations

Astronomical time series from large-scale surveys like LSST are often irregularly sampled and incomplete, posing challenges for classification and anomaly detection. We introduce a new framework based on Neural Stochastic Delay Differential Equations (Neural SDDEs) that combines stochastic modeling with neural networks to capture delayed temporal dynamics and handle irregular observations. Our approach integrates a delay-aware neural architecture, a numerical solver for SDDEs, and mechanisms to robustly learn from noisy, sparse sequences. Experiments on irregularly sampled astronomical data demonstrate strong classification accuracy and effective detection of novel astrophysical events, even with partial labels. This work highlights Neural SDDEs as a principled and practical tool for time series analysis under observational constraints.

TANDEM: Temporal Attention-guided Neural Differential Equations for Missingness in Time Series Classification

Handling missing data in time series classification remains a significant challenge in various domains. Traditional methods often rely on imputation, which may introduce bias or fail to capture the underlying temporal dynamics. In this paper, we propose TANDEM (Temporal Attention-guided Neural Differential Equations for Missingness), an attention-guided neural differential equation framework that effectively classifies time series data with missing values. Our approach integrates raw observation, interpolated control path, and continuous latent dynamics through a novel attention mechanism, allowing the model to focus on the most informative aspects of the data. We evaluate TANDEM on 30 benchmark datasets and a real-world medical dataset, demonstrating its superiority over existing state-of-the-art methods. Our framework not only improves classification accuracy but also provides insights into the handling of missing data, making it a valuable tool in practice.

Stable Neural Stochastic Differential Equations in Analyzing Irregular Time Series Data

Irregular sampling intervals and missing values in real-world time series data present challenges for conventional methods that assume consistent intervals and complete data. Neural Ordinary Differential Equations (Neural ODEs) offer an alternative approach, utilizing neural networks combined with ODE solvers to learn continuous latent representations through parameterized vector fields. Neural Stochastic Differential Equations (Neural SDEs) extend Neural ODEs by incorporating a diffusion term, although this addition is not trivial, particularly when addressing irregular intervals and missing values. Consequently, careful design of drift and diffusion functions is crucial for maintaining stability and enhancing performance, while incautious choices can result in adverse properties such as the absence of strong solutions, stochastic destabilization, or unstable Euler discretizations, significantly affecting Neural SDEs' performance. In this study, we propose three stable classes of Neural SDEs: Langevin-type SDE, Linear Noise SDE, and Geometric SDE. Then, we rigorously demonstrate their robustness in maintaining excellent performance under distribution shift, while effectively preventing overfitting. To assess the effectiveness of our approach, we conduct extensive experiments on four benchmark datasets for interpolation, forecasting, and classification tasks, and analyze the robustness of our methods with 30 public datasets under different missing rates. Our results demonstrate the efficacy of the proposed method in handling real-world irregular time series data.

Invertible Solution of Neural Differential Equations for Analysis of Irregularly-Sampled Time Series

To handle the complexities of irregular and incomplete time series data, we propose an invertible solution of Neural Differential Equations (NDE)-based method. While NDE-based methods are a powerful method for analyzing irregularly-sampled time series, they typically do not guarantee reversible transformations in their standard form. Our method suggests the variation of Neural Controlled Differential Equations (Neural CDEs) with Neural Flow, which ensures invertibility while maintaining a lower computational burden. Additionally, it enables the training of a dual latent space, enhancing the modeling of dynamic temporal dynamics. Our research presents an advanced framework that excels in both classification and interpolation tasks. At the core of our approach is an enhanced dual latent states architecture, carefully designed for high precision across various time series tasks. Empirical analysis demonstrates that our method significantly outperforms existing models. This work significantly advances irregular time series analysis, introducing innovative techniques and offering a versatile tool for diverse practical applications.

Time Delay Estimation of Traffic Congestion Propagation based on Transfer Entropy

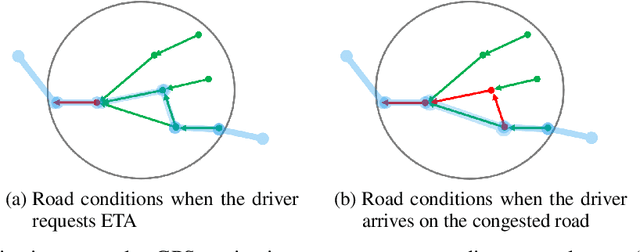
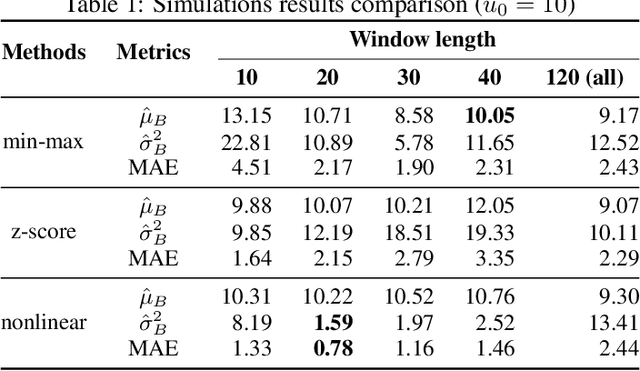
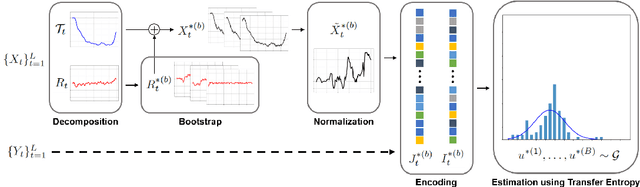
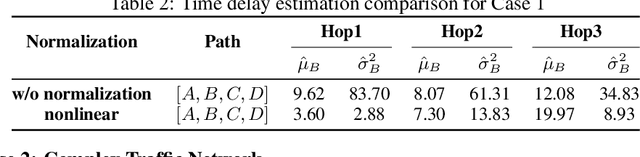
Considering how congestion will propagate in the near future, understanding traffic congestion propagation has become crucial in GPS navigation systems for providing users with a more accurate estimated time of arrival (ETA). However, providing the exact ETA during congestion is a challenge owing to the complex propagation process between roads and high uncertainty regarding the future behavior of the process. Recent studies have focused on finding frequent congestion propagation patterns and determining the propagation probabilities. By contrast, this study proposes a novel time delay estimation method for traffic congestion propagation between roads using lag-specific transfer entropy (TE). Nonlinear normalization with a sliding window is used to effectively reveal the causal relationship between the source and target time series in calculating the TE. Moreover, Markov bootstrap techniques were adopted to quantify the uncertainty in the time delay estimator. To the best of our knowledge, the time delay estimation method presented in this article is the first to determine the time delay between roads for any congestion propagation pattern. The proposed method was validated using simulated data as well as real user trajectory data obtained from a major GPS navigation system applied in South Korea.