Spatio-temporal modeling and forecasting with Fourier neural operators

Spatio-temporal process models are often used for modeling dynamic physical and biological phenomena that evolve across space and time. These phenomena may exhibit environmental heterogeneity and complex interactions that are difficult to capture using traditional statistical process models such as Gaussian processes. This work proposes the use of Fourier neural operators (FNOs) for constructing statistical dynamical spatio-temporal models for forecasting. An FNO is a flexible mapping of functions that approximates the solution operator of possibly unknown linear or non-linear partial differential equations (PDEs) in a computationally efficient manner. It does so using samples of inputs and their respective outputs, and hence explicit knowledge of the underlying PDE is not required. Through simulations from a nonlinear PDE with known solution, we compare FNO forecasts to those from state-of-the-art statistical spatio-temporal-forecasting methods. Further, using sea surface temperature data over the Atlantic Ocean and precipitation data across Europe, we demonstrate the ability of FNO-based dynamic spatio-temporal (DST) statistical modeling to capture complex real-world spatio-temporal dependencies. Using collections of testing instances, we show that the FNO-DST forecasts are accurate with valid uncertainty quantification.

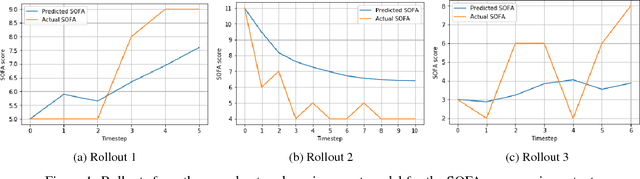
Model-Based Reinforcement Learning for Sepsis Treatment

Sepsis is a dangerous condition that is a leading cause of patient mortality. Treating sepsis is highly challenging, because individual patients respond very differently to medical interventions and there is no universally agreed-upon treatment for sepsis. In this work, we explore the use of continuous state-space model-based reinforcement learning (RL) to discover high-quality treatment policies for sepsis patients. Our quantitative evaluation reveals that by blending the treatment strategy discovered with RL with what clinicians follow, we can obtain improved policies, potentially allowing for better medical treatment for sepsis.

Anytime Monte Carlo

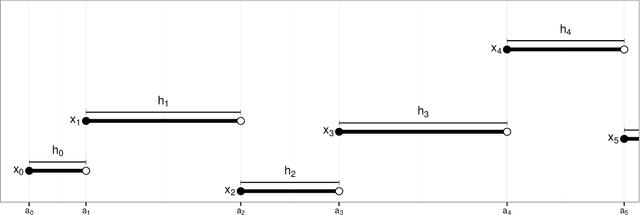
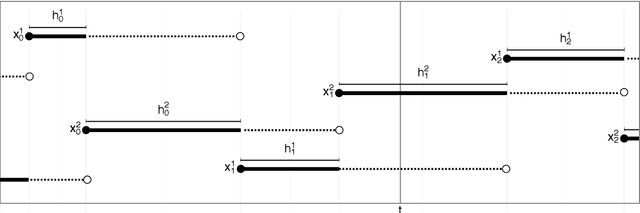
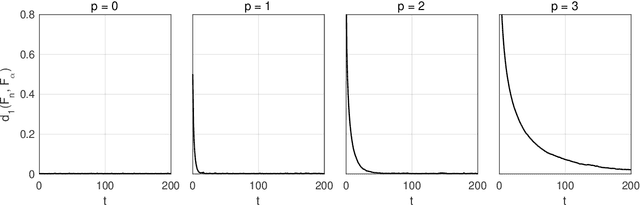
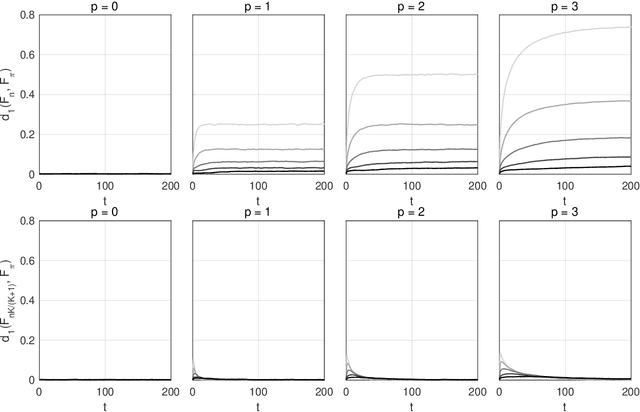
A Monte Carlo algorithm typically simulates some prescribed number of samples, taking some random real time to complete the computations necessary. This work considers the converse: to impose a real-time budget on the computation, so that the number of samples simulated is random. To complicate matters, the real time taken for each simulation may depend on the sample produced, so that the samples themselves are not independent of their number, and a length bias with respect to compute time is apparent. This is especially problematic when a Markov chain Monte Carlo (MCMC) algorithm is used and the final state of the Markov chain---rather than an average over all states---is required. The length bias does not diminish with the compute budget in this case. It occurs, for example, in sequential Monte Carlo (SMC) algorithms. We propose an anytime framework to address the concern, using a continuous-time Markov jump process to study the progress of the computation in real time. We show that the length bias can be eliminated for any MCMC algorithm by using a multiple chain construction. The utility of this construction is demonstrated on a large-scale SMC-squared implementation, using four billion particles distributed across a cluster of 128 graphics processing units on the Amazon EC2 service. The anytime framework imposes a real-time budget on the MCMC move steps within SMC-squared, ensuring that all processors are simultaneously ready for the resampling step, demonstrably reducing wait times and providing substantial control over the total compute budget.