Dynamic Bayesian Learning and Calibration of Spatiotemporal Mechanistic Systems

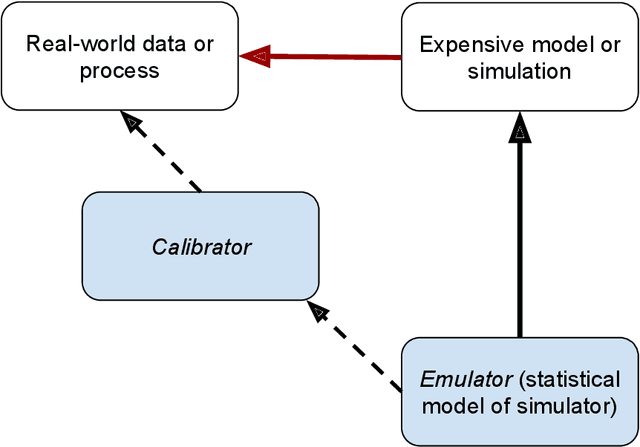
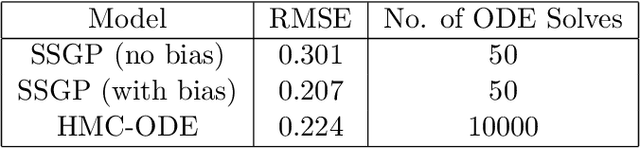
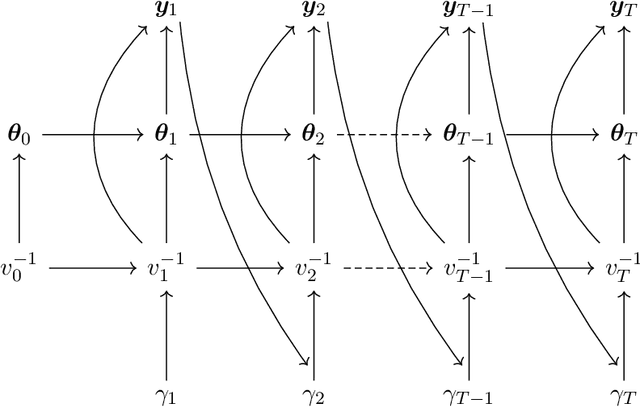
We develop an approach for fully Bayesian learning and calibration of spatiotemporal dynamical mechanistic models based on noisy observations. Calibration is achieved by melding information from observed data with simulated computer experiments from the mechanistic system. The joint melding makes use of both Gaussian and non-Gaussian state-space methods as well as Gaussian process regression. Assuming the dynamical system is controlled by a finite collection of inputs, Gaussian process regression learns the effect of these parameters through a number of training runs, driving the stochastic innovations of the spatiotemporal state-space component. This enables efficient modeling of the dynamics over space and time. Through reduced-rank Gaussian processes and a conjugate model specification, our methodology is applicable to large-scale calibration and inverse problems. Our method is general, extensible, and capable of learning a wide range of dynamical systems with potential model misspecification. We demonstrate this flexibility through solving inverse problems arising in the analysis of ordinary and partial nonlinear differential equations and, in addition, to a black-box computer model generating spatiotemporal dynamics across a network.

Modeling Massive Spatial Datasets Using a Conjugate Bayesian Linear Regression Framework

Geographic Information Systems (GIS) and related technologies have generated substantial interest among statisticians with regard to scalable methodologies for analyzing large spatial datasets. A variety of scalable spatial process models have been proposed that can be easily embedded within a hierarchical modeling framework to carry out Bayesian inference. While the focus of statistical research has mostly been directed toward innovative and more complex model development, relatively limited attention has been accorded to approaches for easily implementable scalable hierarchical models for the practicing scientist or spatial analyst. This article discusses how point-referenced spatial process models can be cast as a conjugate Bayesian linear regression that can rapidly deliver inference on spatial processes. The approach allows exact sampling directly (avoids iterative algorithms such as Markov chain Monte Carlo) from the joint posterior distribution of regression parameters, the latent process and the predictive random variables, and can be easily implemented on statistical programming environments such as R.