Forecasting Residential Heating and Electricity Demand with Scalable, High-Resolution, Open-Source Models

We present a novel framework for high-resolution forecasting of residential heating and electricity demand using probabilistic deep learning models. We focus specifically on providing hourly building-level electricity and heating demand forecasts for the residential sector. Leveraging multimodal building-level information -- including data on building footprint areas, heights, nearby building density, nearby building size, land use patterns, and high-resolution weather data -- and probabilistic modeling, our methods provide granular insights into demand heterogeneity. Validation at the building level underscores a step change improvement in performance relative to NREL's ResStock model, which has emerged as a research community standard for residential heating and electricity demand characterization. In building-level heating and electricity estimation backtests, our probabilistic models respectively achieve RMSE scores 18.3\% and 35.1\% lower than those based on ResStock. By offering an open-source, scalable, high-resolution platform for demand estimation and forecasting, this research advances the tools available for policymakers and grid planners, contributing to the broader effort to decarbonize the U.S. building stock and meeting climate objectives.

Lightweight Data Fusion with Conjugate Mappings

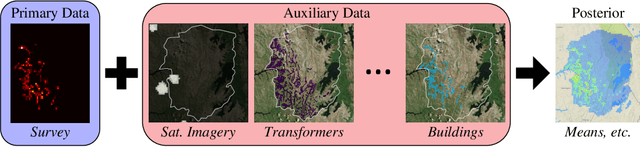
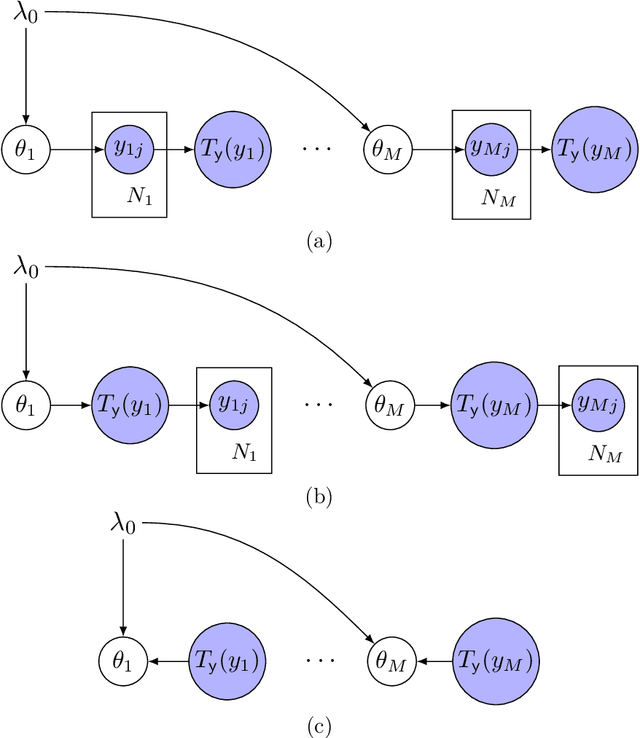
We present an approach to data fusion that combines the interpretability of structured probabilistic graphical models with the flexibility of neural networks. The proposed method, lightweight data fusion (LDF), emphasizes posterior analysis over latent variables using two types of information: primary data, which are well-characterized but with limited availability, and auxiliary data, readily available but lacking a well-characterized statistical relationship to the latent quantity of interest. The lack of a forward model for the auxiliary data precludes the use of standard data fusion approaches, while the inability to acquire latent variable observations severely limits direct application of most supervised learning methods. LDF addresses these issues by utilizing neural networks as conjugate mappings of the auxiliary data: nonlinear transformations into sufficient statistics with respect to the latent variables. This facilitates efficient inference by preserving the conjugacy properties of the primary data and leads to compact representations of the latent variable posterior distributions. We demonstrate the LDF methodology on two challenging inference problems: (1) learning electrification rates in Rwanda from satellite imagery, high-level grid infrastructure, and other sources; and (2) inferring county-level homicide rates in the USA by integrating socio-economic data using a mixture model of multiple conjugate mappings.