Relu and softplus neural nets as zero-sum turn-based games

We show that the output of a ReLU neural network can be interpreted as the value of a zero-sum, turn-based, stopping game, which we call the ReLU net game. The game runs in the direction opposite to that of the network, and the input of the network serves as the terminal reward of the game. In fact, evaluating the network is the same as running the Shapley-Bellman backward recursion for the value of the game. Using the expression of the value of the game as an expected total payoff with respect to the path measure induced by the transition probabilities and a pair of optimal policies, we derive a discrete Feynman-Kac-type path-integral formula for the network output. This game-theoretic representation can be used to derive bounds on the output from bounds on the input, leveraging the monotonicity of Shapley operators, and to verify robustness properties using policies as certificates. Moreover, training the neural network becomes an inverse game problem: given pairs of terminal rewards and corresponding values, one seeks transition probabilities and rewards of a game that reproduces them. Finally, we show that a similar approach applies to neural networks with Softplus activation functions, where the ReLU net game is replaced by its entropic regularization.

A Universal Approximation Result for Difference of log-sum-exp Neural Networks

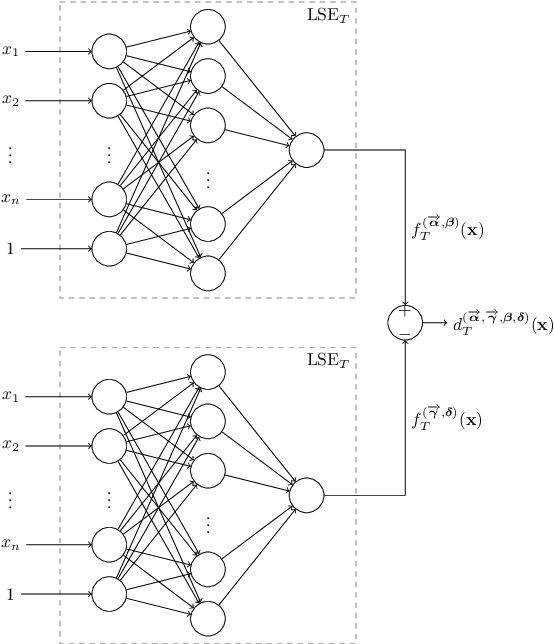
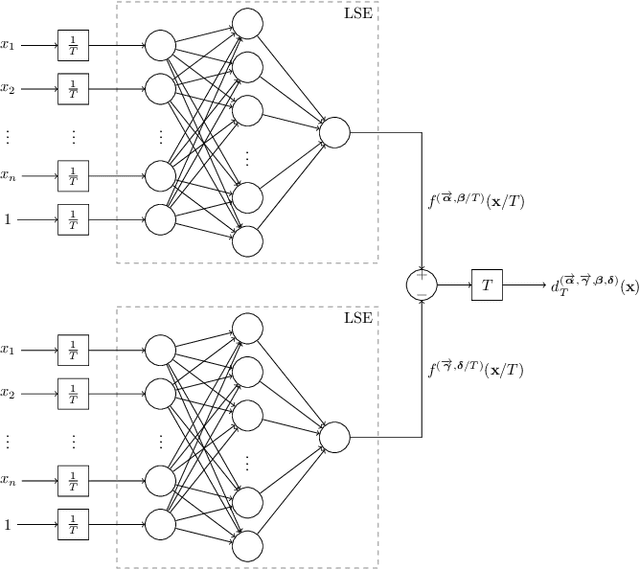
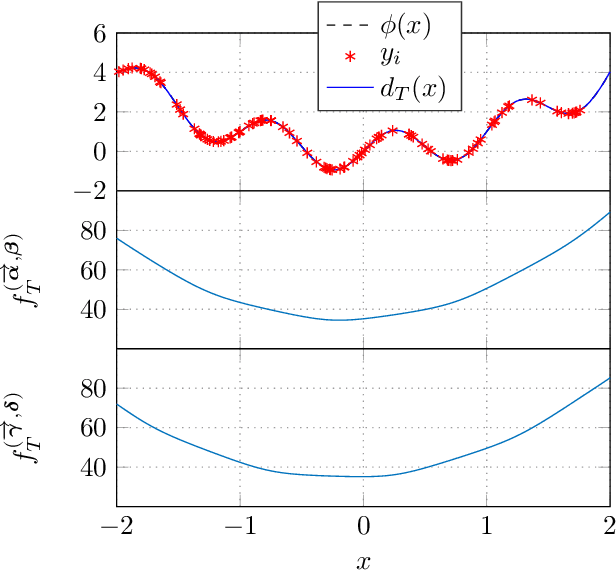
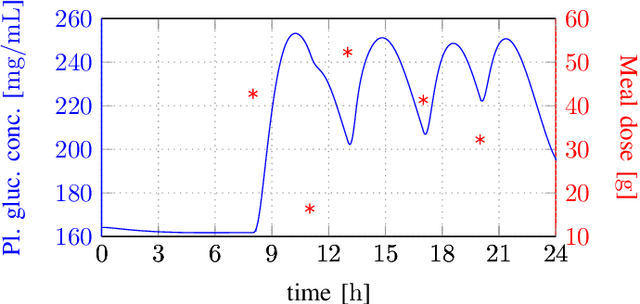
We show that a neural network whose output is obtained as the difference of the outputs of two feedforward networks with exponential activation function in the hidden layer and logarithmic activation function in the output node (LSE networks) is a smooth universal approximator of continuous functions over convex, compact sets. By using a logarithmic transform, this class of networks maps to a family of subtraction-free ratios of generalized posynomials, which we also show to be universal approximators of positive functions over log-convex, compact subsets of the positive orthant. The main advantage of Difference-LSE networks with respect to classical feedforward neural networks is that, after a standard training phase, they provide surrogate models for design that possess a specific difference-of-convex-functions form, which makes them optimizable via relatively efficient numerical methods. In particular, by adapting an existing difference-of-convex algorithm to these models, we obtain an algorithm for performing effective optimization-based design. We illustrate the proposed approach by applying it to data-driven design of a diet for a patient with type-2 diabetes.

Log-sum-exp neural networks and posynomial models for convex and log-log-convex data

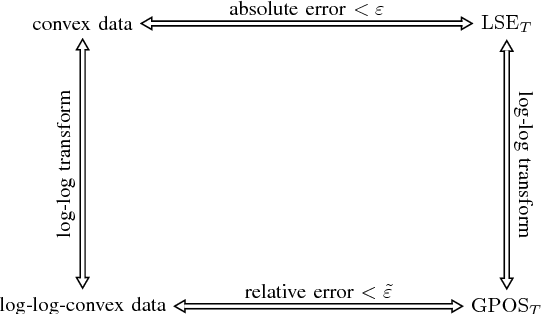
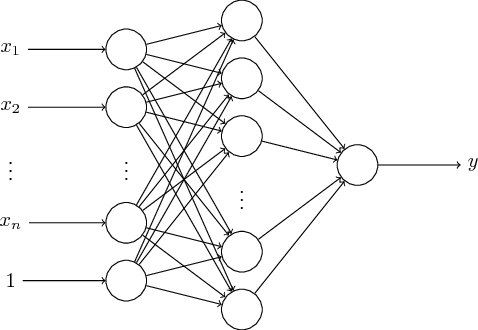
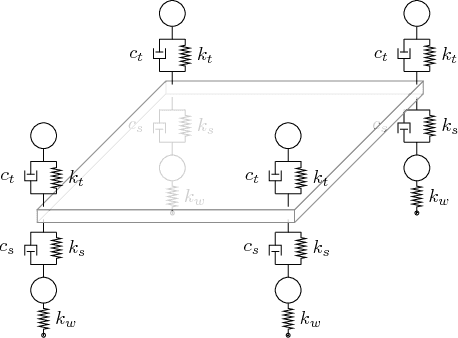
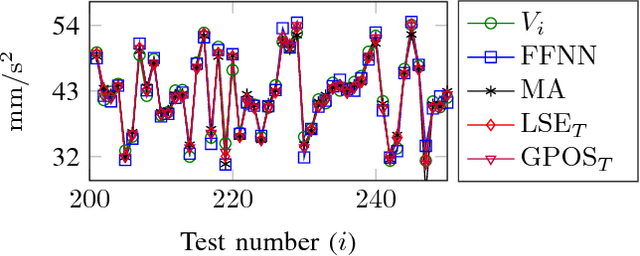
We show that a one-layer feedforward neural network with exponential activation functions in the inner layer and logarithmic activation in the output neuron is a universal approximator of convex functions. Such a network represents a family of scaled log-sum exponential functions, here named LSET. The proof uses a dequantization argument from tropical geometry. Under a suitable exponential transformation LSE maps to a family of generalized posynomial functions GPOST, which we also show to be universal approximators for log-log-convex functions. The key feature of interest in the proposed approach is that, once a LSET network is trained on data, the resulting model is convex in the variables, which makes it readily amenable to efficient design based on convex optimization. Similarly, once a GPOST model is trained on data, it yields a posynomial model that can be efficiently optimized with respect to its variables by using Geometric Programming (GP). Many relevant phenomena in physics and engineering can indeed be modeled, either exactly or approximately, via convex or log-log-convex models. The proposed methodology is illustrated by two numerical examples in which LSET and GPOST models are used to first approximate data gathered from the simulations of two physical processes (the vibration from a vehicle suspension system, and the peak power generated by the combustion of propane), and to later optimize these models.