Srikanth Namuduri
Faster Deep Ensemble Averaging for Quantification of DNA Damage from Comet Assay Images With Uncertainty Estimates
Dec 23, 2021
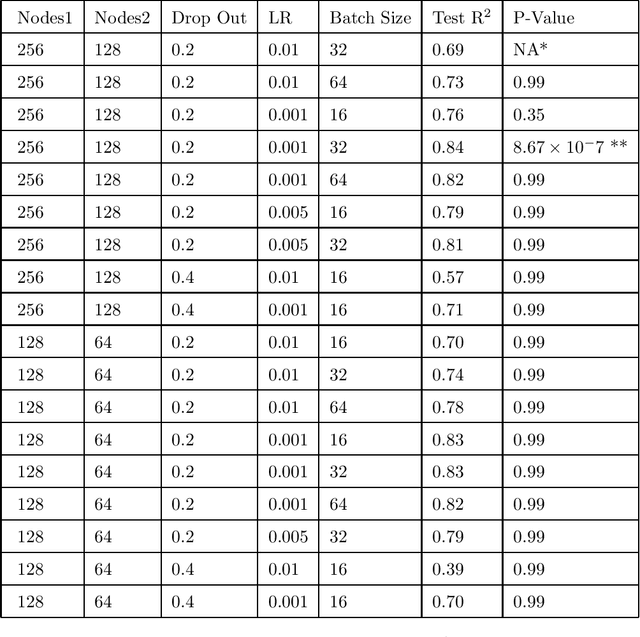

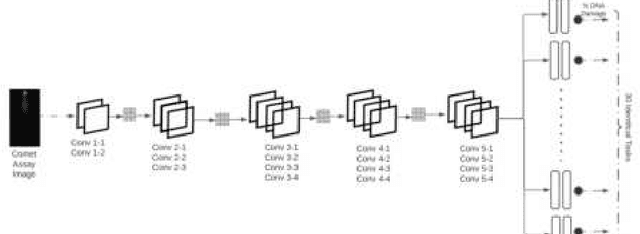
Abstract:Several neurodegenerative diseases involve the accumulation of cellular DNA damage. Comet assays are a popular way of estimating the extent of DNA damage. Current literature on the use of deep learning to quantify DNA damage presents an empirical approach to hyper-parameter optimization and does not include uncertainty estimates. Deep ensemble averaging is a standard approach to estimating uncertainty but it requires several iterations of network training, which makes it time-consuming. Here we present an approach to quantify the extent of DNA damage that combines deep learning with a rigorous and comprehensive method to optimize the hyper-parameters with the help of statistical tests. We also use an architecture that allows for a faster computation of deep ensemble averaging and performs statistical tests applicable to networks using transfer learning. We applied our approach to a comet assay dataset with more than 1300 images and achieved an $R^2$ of 0.84, where the output included the confidence interval for each prediction. The proposed architecture is an improvement over the current approaches since it speeds up the uncertainty estimation by 30X while being statistically more rigorous.
Quantum Generalized Linear Models
May 01, 2019
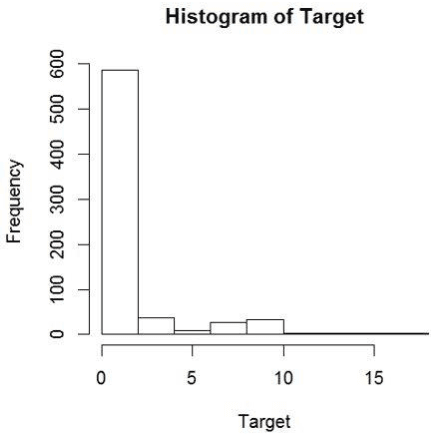
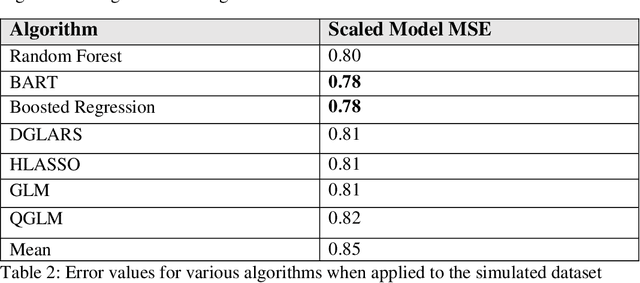
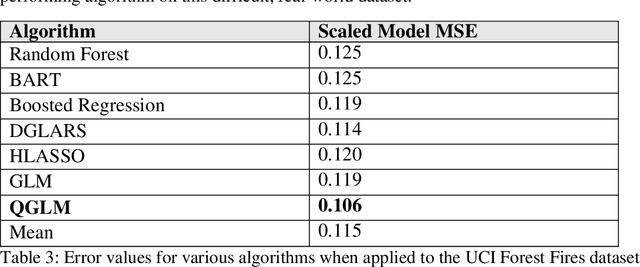
Abstract:Generalized linear models (GLM) are link function based statistical models. Many supervised learning algorithms are extensions of GLMs and have link functions built into the algorithm to model different outcome distributions. There are two major drawbacks when using this approach in applications using real world datasets. One is that none of the link functions available in the popular packages is a good fit for the data. Second, it is computationally inefficient and impractical to test all the possible distributions to find the optimum one. In addition, many GLMs and their machine learning extensions struggle on problems of overdispersion in Tweedie distributions. In this paper we propose a quantum extension to GLM that overcomes these drawbacks. A quantum gate with non-Gaussian transformation can be used to continuously deform the outcome distribution from known results. In doing so, we eliminate the need for a link function. Further, by using an algorithm that superposes all possible distributions to collapse to fit a dataset, we optimize the model in a computationally efficient way. We provide an initial proof-of-concept by testing this approach on both a simulation of overdispersed data and then on a benchmark dataset, which is quite overdispersed, and achieved state of the art results. This is a game changer in several applied fields, such as part failure modeling, medical research, actuarial science, finance and many other fields where Tweedie regression and overdispersion are ubiquitous.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge