Soronzonbold Otgonbaatar
Quantum-inspired tensor network for Earth science
Jan 15, 2023Abstract:Deep Learning (DL) is one of many successful methodologies to extract informative patterns and insights from ever increasing noisy large-scale datasets (in our case, satellite images). However, DL models consist of a few thousand to millions of training parameters, and these training parameters require tremendous amount of electrical power for extracting informative patterns from noisy large-scale datasets (e.g., computationally expensive). Hence, we employ a quantum-inspired tensor network for compressing trainable parameters of physics-informed neural networks (PINNs) in Earth science. PINNs are DL models penalized by enforcing the law of physics; in particular, the law of physics is embedded in DL models. In addition, we apply tensor decomposition to HyperSpectral Images (HSIs) to improve their spectral resolution. A quantum-inspired tensor network is also the native formulation to efficiently represent and train quantum machine learning models on big datasets on GPU tensor cores. Furthermore, the key contribution of this paper is twofold: (I) we reduced a number of trainable parameters of PINNs by using a quantum-inspired tensor network, and (II) we improved the spectral resolution of remotely-sensed images by employing tensor decomposition. As a benchmark PDE, we solved Burger's equation. As practical satellite data, we employed HSIs of Indian Pine, USA and of Pavia University, Italy.
* This article is submitted to IGARSS 2023 conference
Coreset of Hyperspectral Images on Small Quantum Computer
Apr 12, 2022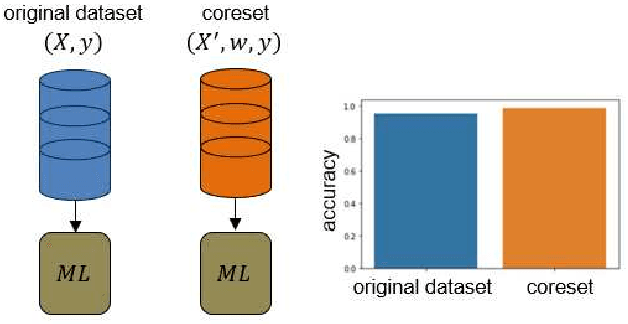
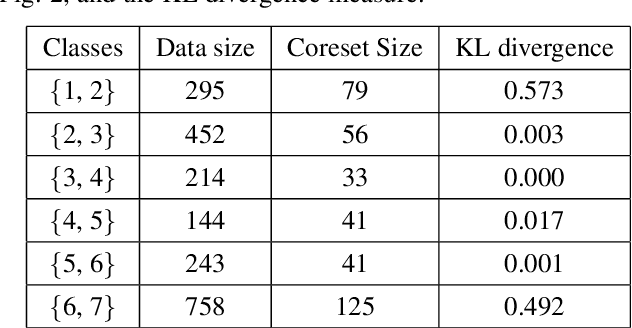
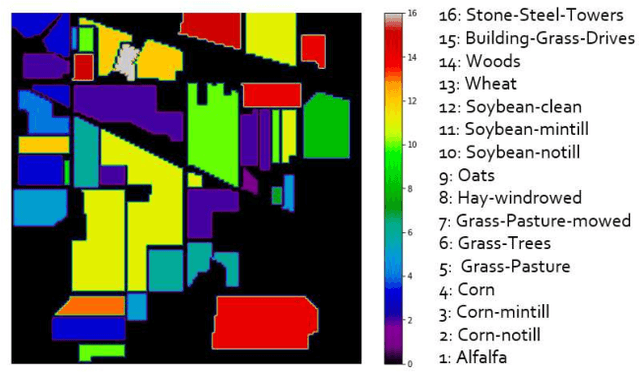
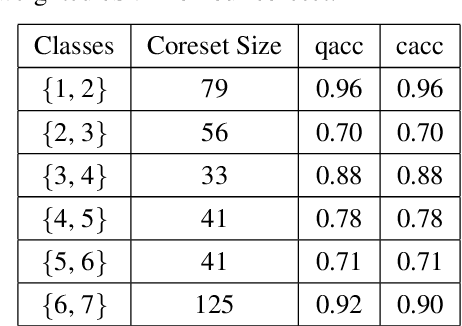
Abstract:Machine Learning (ML) techniques are employed to analyze and process big Remote Sensing (RS) data, and one well-known ML technique is a Support Vector Machine (SVM). An SVM is a quadratic programming (QP) problem, and a D-Wave quantum annealer (D-Wave QA) promises to solve this QP problem more efficiently than a conventional computer. However, the D-Wave QA cannot solve directly the SVM due to its very few input qubits. Hence, we use a coreset ("core of a dataset") of given EO data for training an SVM on this small D-Wave QA. The coreset is a small, representative weighted subset of an original dataset, and any training models generate competitive classes by using the coreset in contrast to by using its original dataset. We measured the closeness between an original dataset and its coreset by employing a Kullback-Leibler (KL) divergence measure. Moreover, we trained the SVM on the coreset data by using both a D-Wave QA and a conventional method. We conclude that the coreset characterizes the original dataset with very small KL divergence measure. In addition, we present our KL divergence results for demonstrating the closeness between our original data and its coreset. As practical RS data, we use Hyperspectral Image (HSI) of Indian Pine, USA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge