Intrinsic training dynamics of deep neural networks

A fundamental challenge in the theory of deep learning is to understand whether gradient-based training in high-dimensional parameter spaces can be captured by simpler, lower-dimensional structures, leading to so-called implicit bias. As a stepping stone, we study when a gradient flow on a high-dimensional variable $\theta$ implies an intrinsic gradient flow on a lower-dimensional variable $z = \phi(\theta)$, for an architecture-related function $\phi$. We express a so-called intrinsic dynamic property and show how it is related to the study of conservation laws associated with the factorization $\phi$. This leads to a simple criterion based on the inclusion of kernels of linear maps which yields a necessary condition for this property to hold. We then apply our theory to general ReLU networks of arbitrary depth and show that, for any initialization, it is possible to rewrite the flow as an intrinsic dynamic in a lower dimension that depends only on $z$ and the initialization, when $\phi$ is the so-called path-lifting. In the case of linear networks with $\phi$ the product of weight matrices, so-called balanced initializations are also known to enable such a dimensionality reduction; we generalize this result to a broader class of {\em relaxed balanced} initializations, showing that, in certain configurations, these are the \emph{only} initializations that ensure the intrinsic dynamic property. Finally, for the linear neural ODE associated with the limit of infinitely deep linear networks, with relaxed balanced initialization, we explicitly express the corresponding intrinsic dynamics.

Transformative or Conservative? Conservation laws for ResNets and Transformers

While conservation laws in gradient flow training dynamics are well understood for (mostly shallow) ReLU and linear networks, their study remains largely unexplored for more practical architectures. This paper bridges this gap by deriving and analyzing conservation laws for modern architectures, with a focus on convolutional ResNets and Transformer networks. For this, we first show that basic building blocks such as ReLU (or linear) shallow networks, with or without convolution, have easily expressed conservation laws, and no more than the known ones. In the case of a single attention layer, we also completely describe all conservation laws, and we show that residual blocks have the same conservation laws as the same block without a skip connection. We then introduce the notion of conservation laws that depend only on a subset of parameters (corresponding e.g. to a pair of consecutive layers, to a residual block, or to an attention layer). We demonstrate that the characterization of such laws can be reduced to the analysis of the corresponding building block in isolation. Finally, we examine how these newly discovered conservation principles, initially established in the continuous gradient flow regime, persist under discrete optimization dynamics, particularly in the context of Stochastic Gradient Descent (SGD).

Keep the Momentum: Conservation Laws beyond Euclidean Gradient Flows

Conservation laws are well-established in the context of Euclidean gradient flow dynamics, notably for linear or ReLU neural network training. Yet, their existence and principles for non-Euclidean geometries and momentum-based dynamics remain largely unknown. In this paper, we characterize "all" conservation laws in this general setting. In stark contrast to the case of gradient flows, we prove that the conservation laws for momentum-based dynamics exhibit temporal dependence. Additionally, we often observe a "conservation loss" when transitioning from gradient flow to momentum dynamics. Specifically, for linear networks, our framework allows us to identify all momentum conservation laws, which are less numerous than in the gradient flow case except in sufficiently over-parameterized regimes. With ReLU networks, no conservation law remains. This phenomenon also manifests in non-Euclidean metrics, used e.g. for Nonnegative Matrix Factorization (NMF): all conservation laws can be determined in the gradient flow context, yet none persists in the momentum case.

Abide by the Law and Follow the Flow: Conservation Laws for Gradient Flows

Understanding the geometric properties of gradient descent dynamics is a key ingredient in deciphering the recent success of very large machine learning models. A striking observation is that trained over-parameterized models retain some properties of the optimization initialization. This "implicit bias" is believed to be responsible for some favorable properties of the trained models and could explain their good generalization properties. The purpose of this article is threefold. First, we rigorously expose the definition and basic properties of "conservation laws", which are maximal sets of independent quantities conserved during gradient flows of a given model (e.g. of a ReLU network with a given architecture) with any training data and any loss. Then we explain how to find the exact number of these quantities by performing finite-dimensional algebraic manipulations on the Lie algebra generated by the Jacobian of the model. Finally, we provide algorithms (implemented in SageMath) to: a) compute a family of polynomial laws; b) compute the number of (not necessarily polynomial) conservation laws. We provide showcase examples that we fully work out theoretically. Besides, applying the two algorithms confirms for a number of ReLU network architectures that all known laws are recovered by the algorithm, and that there are no other laws. Such computational tools pave the way to understanding desirable properties of optimization initialization in large machine learning models.

Fast Multiscale Diffusion on Graphs

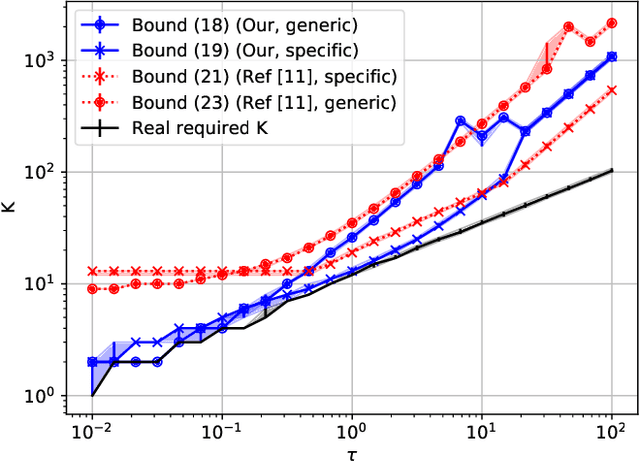
Diffusing a graph signal at multiple scales requires computing the action of the exponential of several multiples of the Laplacian matrix. We tighten a bound on the approximation error of truncated Chebyshev polynomial approximations of the exponential, hence significantly improving a priori estimates of the polynomial order for a prescribed error. We further exploit properties of these approximations to factorize the computation of the action of the diffusion operator over multiple scales, thus reducing drastically its computational cost.