Multi-view Information Bottleneck Without Variational Approximation

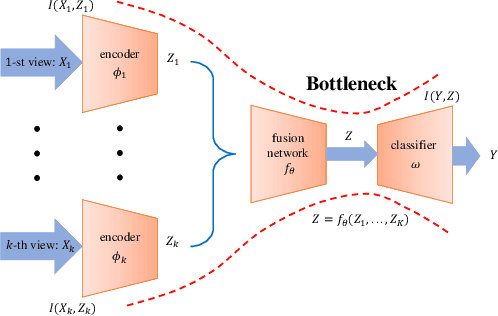
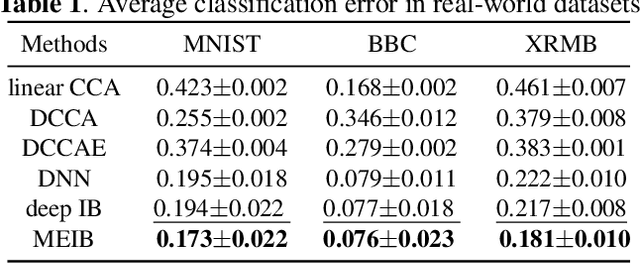
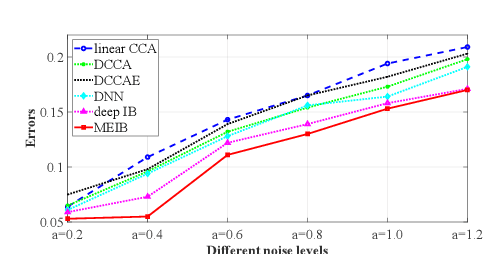
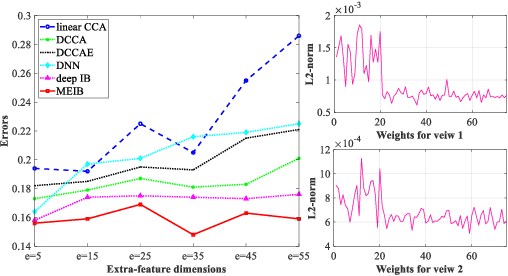
By "intelligently" fusing the complementary information across different views, multi-view learning is able to improve the performance of classification tasks. In this work, we extend the information bottleneck principle to a supervised multi-view learning scenario and use the recently proposed matrix-based R{\'e}nyi's $\alpha$-order entropy functional to optimize the resulting objective directly, without the necessity of variational approximation or adversarial training. Empirical results in both synthetic and real-world datasets suggest that our method enjoys improved robustness to noise and redundant information in each view, especially given limited training samples. Code is available at~\url{https://github.com/archy666/MEIB}.

R2-Trans:Fine-Grained Visual Categorization with Redundancy Reduction

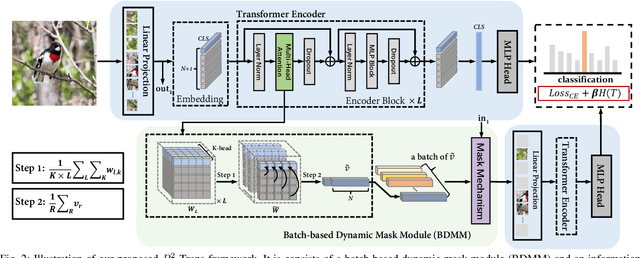
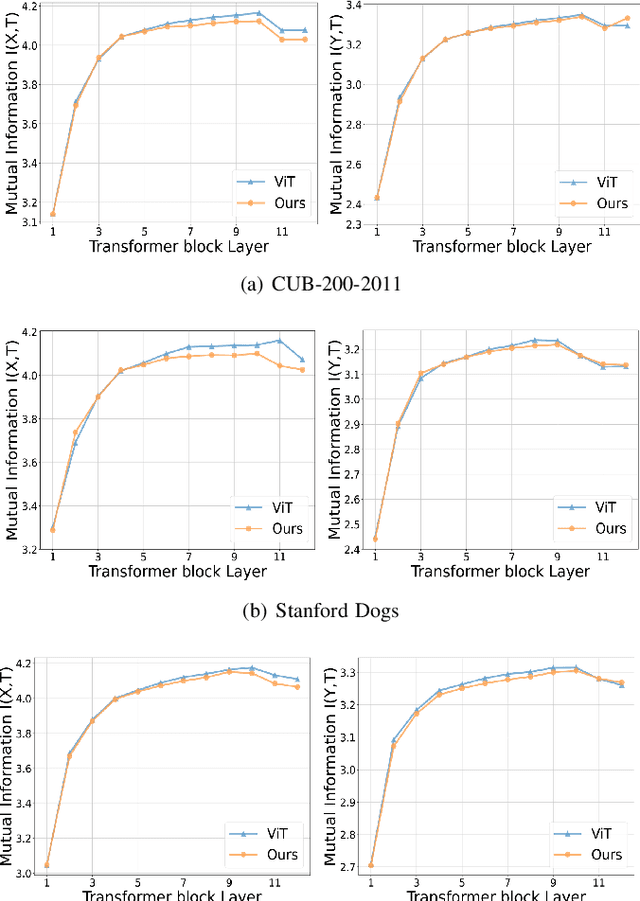
Fine-grained visual categorization (FGVC) aims to discriminate similar subcategories, whose main challenge is the large intraclass diversities and subtle inter-class differences. Existing FGVC methods usually select discriminant regions found by a trained model, which is prone to neglect other potential discriminant information. On the other hand, the massive interactions between the sequence of image patches in ViT make the resulting class-token contain lots of redundant information, which may also impacts FGVC performance. In this paper, we present a novel approach for FGVC, which can simultaneously make use of partial yet sufficient discriminative information in environmental cues and also compress the redundant information in class-token with respect to the target. Specifically, our model calculates the ratio of high-weight regions in a batch, adaptively adjusts the masking threshold and achieves moderate extraction of background information in the input space. Moreover, we also use the Information Bottleneck~(IB) approach to guide our network to learn a minimum sufficient representations in the feature space. Experimental results on three widely-used benchmark datasets verify that our approach can achieve outperforming performance than other state-of-the-art approaches and baseline models.

Deep Deterministic Independent Component Analysis for Hyperspectral Unmixing

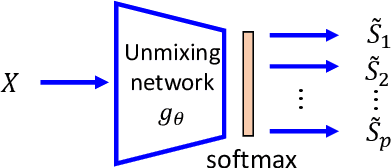
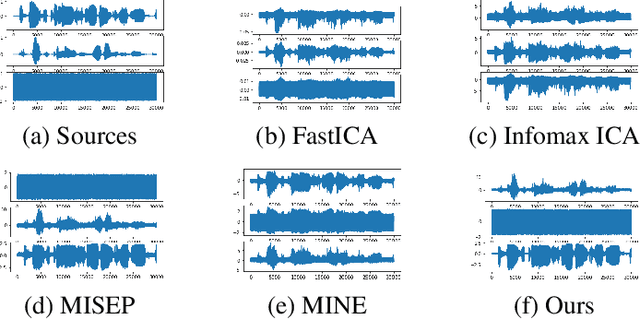
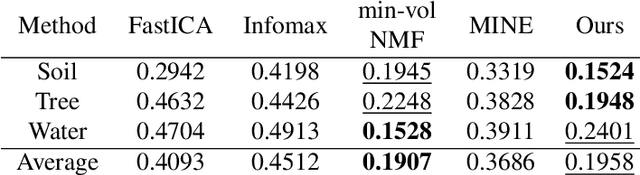
We develop a new neural network based independent component analysis (ICA) method by directly minimizing the dependence amongst all extracted components. Using the matrix-based R{\'e}nyi's $\alpha$-order entropy functional, our network can be directly optimized by stochastic gradient descent (SGD), without any variational approximation or adversarial training. As a solid application, we evaluate our ICA in the problem of hyperspectral unmixing (HU) and refute a statement that "\emph{ICA does not play a role in unmixing hyperspectral data}", which was initially suggested by \cite{nascimento2005does}. Code and additional remarks of our DDICA is available at https://github.com/hongmingli1995/DDICA.

Computationally Efficient Approximations for Matrix-based Renyi's Entropy

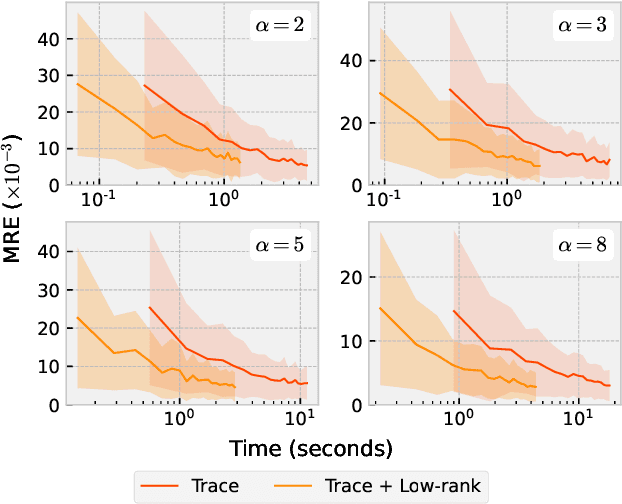
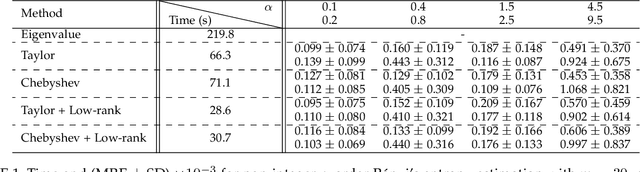
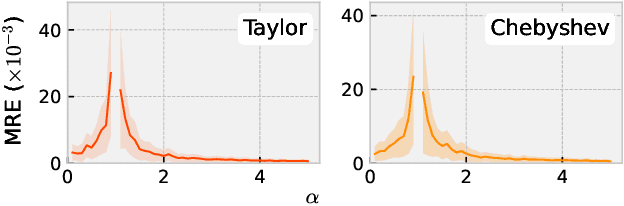
The recently developed matrix based Renyi's entropy enables measurement of information in data simply using the eigenspectrum of symmetric positive semi definite (PSD) matrices in reproducing kernel Hilbert space, without estimation of the underlying data distribution. This intriguing property makes the new information measurement widely adopted in multiple statistical inference and learning tasks. However, the computation of such quantity involves the trace operator on a PSD matrix $G$ to power $\alpha$(i.e., $tr(G^\alpha)$), with a normal complexity of nearly $O(n^3)$, which severely hampers its practical usage when the number of samples (i.e., $n$) is large. In this work, we present computationally efficient approximations to this new entropy functional that can reduce its complexity to even significantly less than $O(n^2)$. To this end, we first develop randomized approximations to $\tr(\G^\alpha)$ that transform the trace estimation into matrix-vector multiplications problem. We extend such strategy for arbitrary values of $\alpha$ (integer or non-integer). We then establish the connection between the matrix-based Renyi's entropy and PSD matrix approximation, which enables us to exploit both clustering and block low-rank structure of $\G$ to further reduce the computational cost. We theoretically provide approximation accuracy guarantees and illustrate the properties of different approximations. Large-scale experimental evaluations on both synthetic and real-world data corroborate our theoretical findings, showing promising speedup with negligible loss in accuracy.

Gated Information Bottleneck for Generalization in Sequential Environments

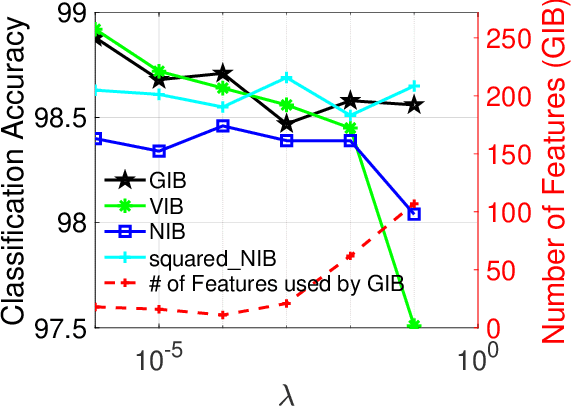
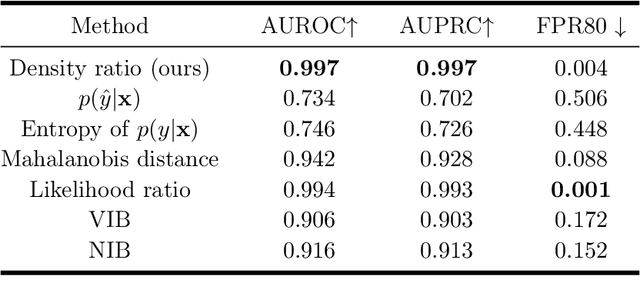
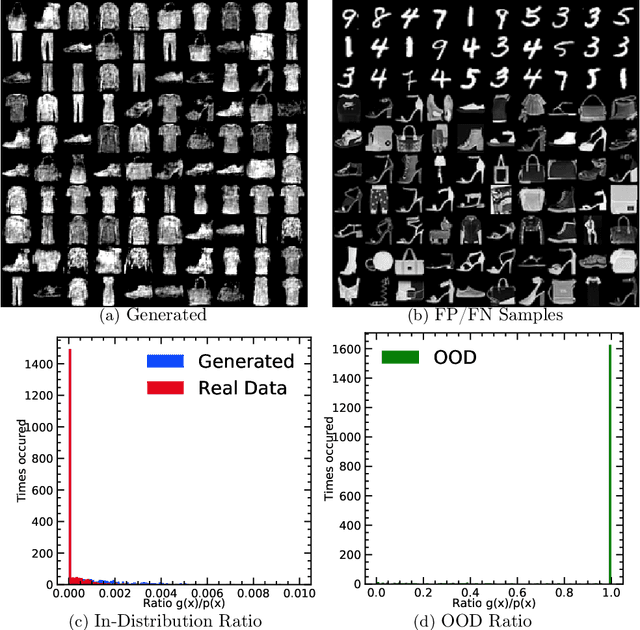
Deep neural networks suffer from poor generalization to unseen environments when the underlying data distribution is different from that in the training set. By learning minimum sufficient representations from training data, the information bottleneck (IB) approach has demonstrated its effectiveness to improve generalization in different AI applications. In this work, we propose a new neural network-based IB approach, termed gated information bottleneck (GIB), that dynamically drops spurious correlations and progressively selects the most task-relevant features across different environments by a trainable soft mask (on raw features). GIB enjoys a simple and tractable objective, without any variational approximation or distributional assumption. We empirically demonstrate the superiority of GIB over other popular neural network-based IB approaches in adversarial robustness and out-of-distribution (OOD) detection. Meanwhile, we also establish the connection between IB theory and invariant causal representation learning, and observed that GIB demonstrates appealing performance when different environments arrive sequentially, a more practical scenario where invariant risk minimization (IRM) fails. Code of GIB is available at https://github.com/falesiani/GIB

Information Theoretic Structured Generative Modeling

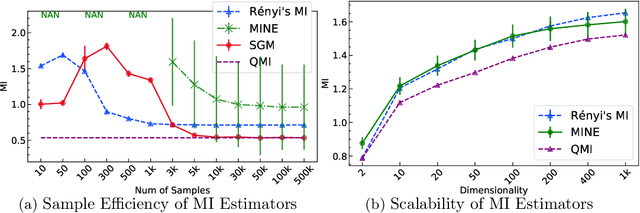
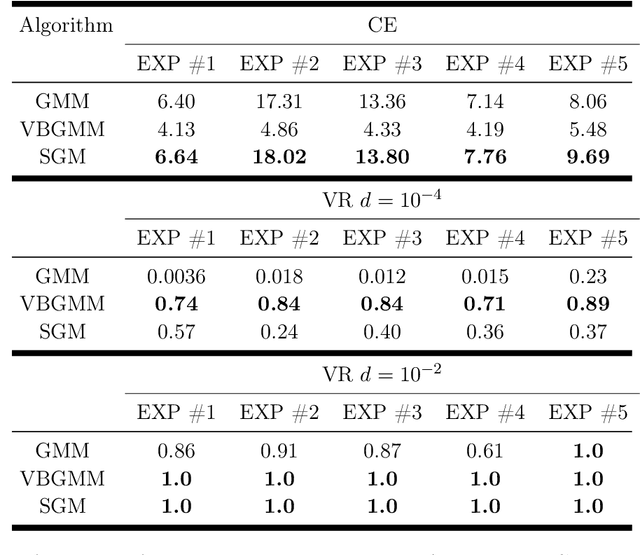
R\'enyi's information provides a theoretical foundation for tractable and data-efficient non-parametric density estimation, based on pair-wise evaluations in a reproducing kernel Hilbert space (RKHS). This paper extends this framework to parametric probabilistic modeling, motivated by the fact that R\'enyi's information can be estimated in closed-form for Gaussian mixtures. Based on this special connection, a novel generative model framework called the structured generative model (SGM) is proposed that makes straightforward optimization possible, because costs are scale-invariant, avoiding high gradient variance while imposing less restrictions on absolute continuity, which is a huge advantage in parametric information theoretic optimization. The implementation employs a single neural network driven by an orthonormal input appended to a single white noise source adapted to learn an infinite Gaussian mixture model (IMoG), which provides an empirically tractable model distribution in low dimensions. To train SGM, we provide three novel variational cost functions, based on R\'enyi's second-order entropy and divergence, to implement minimization of cross-entropy, minimization of variational representations of $f$-divergence, and maximization of the evidence lower bound (conditional probability). We test the framework for estimation of mutual information and compare the results with the mutual information neural estimation (MINE), for density estimation, for conditional probability estimation in Markov models as well as for training adversarial networks. Our preliminary results show that SGM significantly improves MINE estimation in terms of data efficiency and variance, conventional and variational Gaussian mixture models, as well as the performance of generative adversarial networks.

Learning to Transfer with von Neumann Conditional Divergence

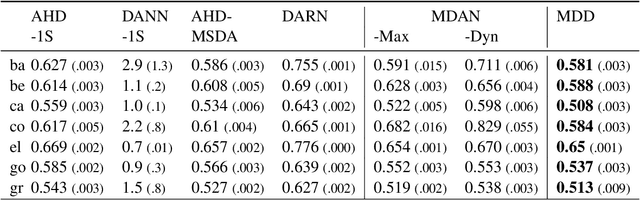
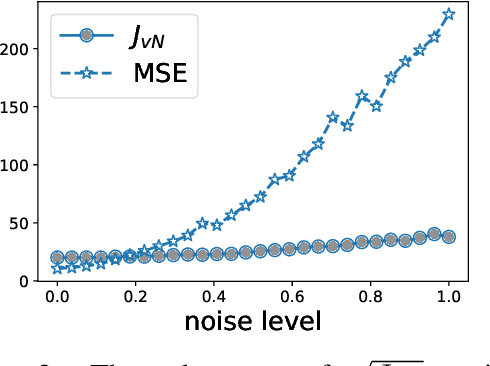
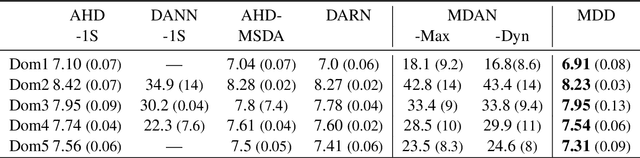
The similarity of feature representations plays a pivotal role in the success of domain adaptation and generalization. Feature similarity includes both the invariance of marginal distributions and the closeness of conditional distributions given the desired response $y$ (e.g., class labels). Unfortunately, traditional methods always learn such features without fully taking into consideration the information in $y$, which in turn may lead to a mismatch of the conditional distributions or the mix-up of discriminative structures underlying data distributions. In this work, we introduce the recently proposed von Neumann conditional divergence to improve the transferability across multiple domains. We show that this new divergence is differentiable and eligible to easily quantify the functional dependence between features and $y$. Given multiple source tasks, we integrate this divergence to capture discriminative information in $y$ and design novel learning objectives assuming those source tasks are observed either simultaneously or sequentially. In both scenarios, we obtain favorable performance against state-of-the-art methods in terms of smaller generalization error on new tasks and less catastrophic forgetting on source tasks (in the sequential setup).

Deep Deterministic Information Bottleneck with Matrix-based Entropy Functional

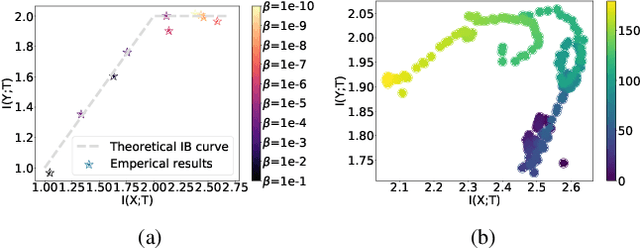
We introduce the matrix-based Renyi's $\alpha$-order entropy functional to parameterize Tishby et al. information bottleneck (IB) principle with a neural network. We term our methodology Deep Deterministic Information Bottleneck (DIB), as it avoids variational inference and distribution assumption. We show that deep neural networks trained with DIB outperform the variational objective counterpart and those that are trained with other forms of regularization, in terms of generalization performance and robustness to adversarial attack.Code available at https://github.com/yuxi120407/DIB

Measuring Dependence with Matrix-based Entropy Functional

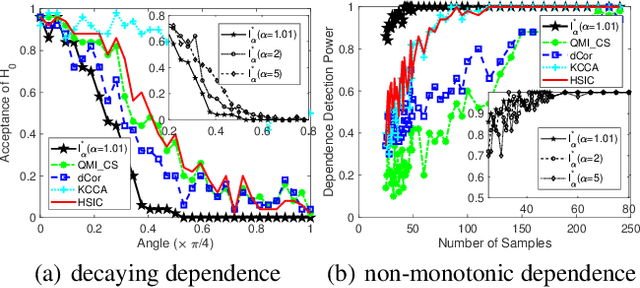
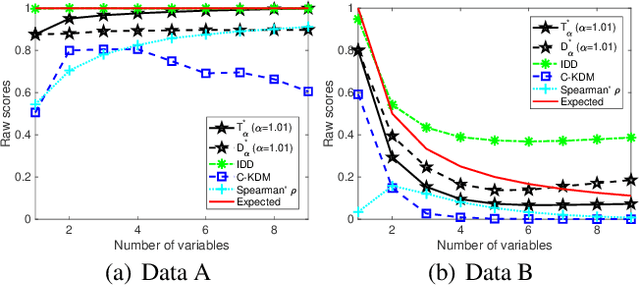
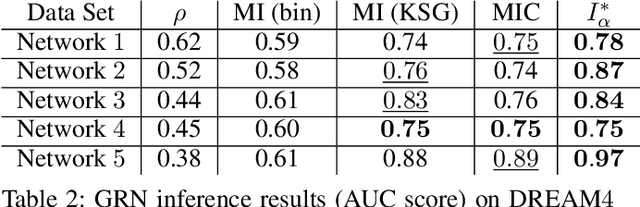
Measuring the dependence of data plays a central role in statistics and machine learning. In this work, we summarize and generalize the main idea of existing information-theoretic dependence measures into a higher-level perspective by the Shearer's inequality. Based on our generalization, we then propose two measures, namely the matrix-based normalized total correlation ($T_\alpha^*$) and the matrix-based normalized dual total correlation ($D_\alpha^*$), to quantify the dependence of multiple variables in arbitrary dimensional space, without explicit estimation of the underlying data distributions. We show that our measures are differentiable and statistically more powerful than prevalent ones. We also show the impact of our measures in four different machine learning problems, namely the gene regulatory network inference, the robust machine learning under covariate shift and non-Gaussian noises, the subspace outlier detection, and the understanding of the learning dynamics of convolutional neural networks (CNNs), to demonstrate their utilities, advantages, as well as implications to those problems. Code of our dependence measure is available at: https://bit.ly/AAAI-dependence

Modular-Relatedness for Continual Learning

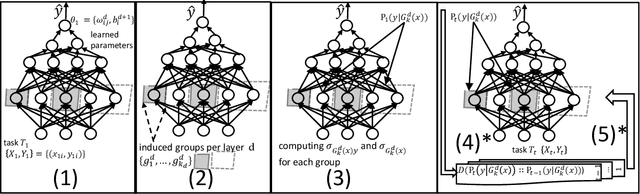
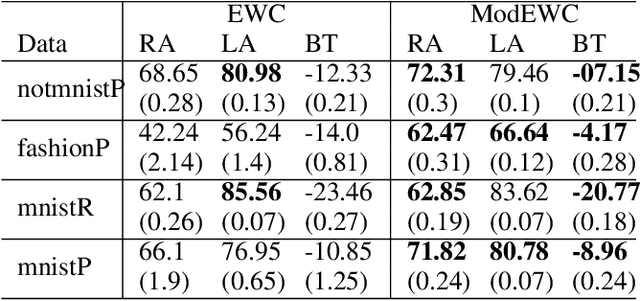
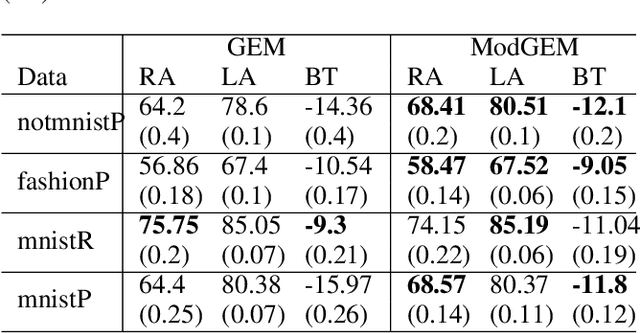
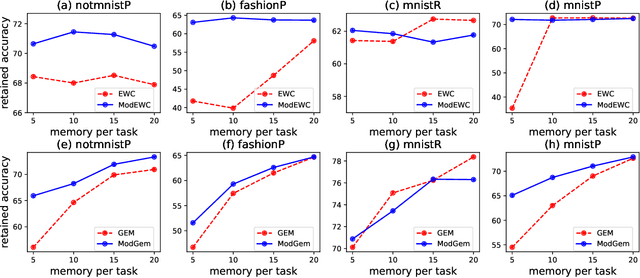
In this paper, we propose a continual learning (CL) technique that is beneficial to sequential task learners by improving their retained accuracy and reducing catastrophic forgetting. The principal target of our approach is the automatic extraction of modular parts of the neural network and then estimating the relatedness between the tasks given these modular components. This technique is applicable to different families of CL methods such as regularization-based (e.g., the Elastic Weight Consolidation) or the rehearsal-based (e.g., the Gradient Episodic Memory) approaches where episodic memory is needed. Empirical results demonstrate remarkable performance gain (in terms of robustness to forgetting) for methods such as EWC and GEM based on our technique, especially when the memory budget is very limited.