CATS-V2V: A Real-World Vehicle-to-Vehicle Cooperative Perception Dataset with Complex Adverse Traffic Scenarios

Vehicle-to-Vehicle (V2V) cooperative perception has great potential to enhance autonomous driving performance by overcoming perception limitations in complex adverse traffic scenarios (CATS). Meanwhile, data serves as the fundamental infrastructure for modern autonomous driving AI. However, due to stringent data collection requirements, existing datasets focus primarily on ordinary traffic scenarios, constraining the benefits of cooperative perception. To address this challenge, we introduce CATS-V2V, the first-of-its-kind real-world dataset for V2V cooperative perception under complex adverse traffic scenarios. The dataset was collected by two hardware time-synchronized vehicles, covering 10 weather and lighting conditions across 10 diverse locations. The 100-clip dataset includes 60K frames of 10 Hz LiDAR point clouds and 1.26M multi-view 30 Hz camera images, along with 750K anonymized yet high-precision RTK-fixed GNSS and IMU records. Correspondingly, we provide time-consistent 3D bounding box annotations for objects, as well as static scenes to construct a 4D BEV representation. On this basis, we propose a target-based temporal alignment method, ensuring that all objects are precisely aligned across all sensor modalities. We hope that CATS-V2V, the largest-scale, most supportive, and highest-quality dataset of its kind to date, will benefit the autonomous driving community in related tasks.

FlowVAT: Normalizing Flow Variational Inference with Affine-Invariant Tempering

Multi-modal and high-dimensional posteriors present significant challenges for variational inference, causing mode-seeking behavior and collapse despite the theoretical expressiveness of normalizing flows. Traditional annealing methods require temperature schedules and hyperparameter tuning, falling short of the goal of truly black-box variational inference. We introduce FlowVAT, a conditional tempering approach for normalizing flow variational inference that addresses these limitations. Our method tempers both the base and target distributions simultaneously, maintaining affine-invariance under tempering. By conditioning the normalizing flow on temperature, we leverage overparameterized neural networks' generalization capabilities to train a single flow representing the posterior across a range of temperatures. This preserves modes identified at higher temperatures when sampling from the variational posterior at $T = 1$, mitigating standard variational methods' mode-seeking behavior. In experiments with 2, 10, and 20 dimensional multi-modal distributions, FlowVAT outperforms traditional and adaptive annealing methods, finding more modes and achieving better ELBO values, particularly in higher dimensions where existing approaches fail. Our method requires minimal hyperparameter tuning and does not require an annealing schedule, advancing toward fully-automatic black-box variational inference for complicated posteriors.

Fast Inference Using Automatic Differentiation and Neural Transport in Astroparticle Physics

Multi-dimensional parameter spaces are commonly encountered in astroparticle physics theories that attempt to capture novel phenomena. However, they often possess complicated posterior geometries that are expensive to traverse using techniques traditional to this community. Effectively sampling these spaces is crucial to bridge the gap between experiment and theory. Several recent innovations, which are only beginning to make their way into this field, have made navigating such complex posteriors possible. These include GPU acceleration, automatic differentiation, and neural-network-guided reparameterization. We apply these advancements to astroparticle physics experimental results in the context of novel neutrino physics and benchmark their performances against traditional nested sampling techniques. Compared to nested sampling alone, we find that these techniques increase performance for both nested sampling and Hamiltonian Monte Carlo, accelerating inference by factors of $\sim 100$ and $\sim 60$, respectively. As nested sampling also evaluates the Bayesian evidence, these advancements can be exploited to improve model comparison performance while retaining compatibility with existing implementations that are widely used in the natural sciences.

Domain-informed neural networks for interaction localization within astroparticle experiments

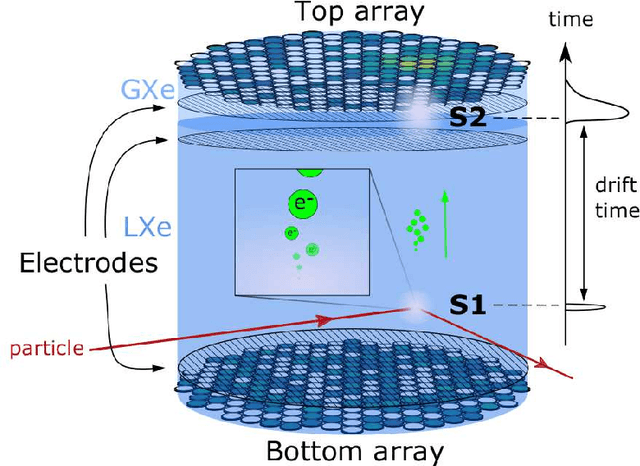
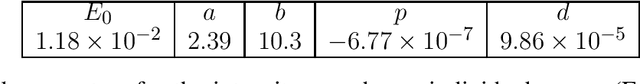
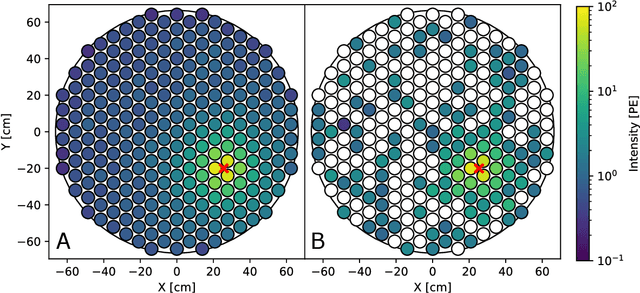
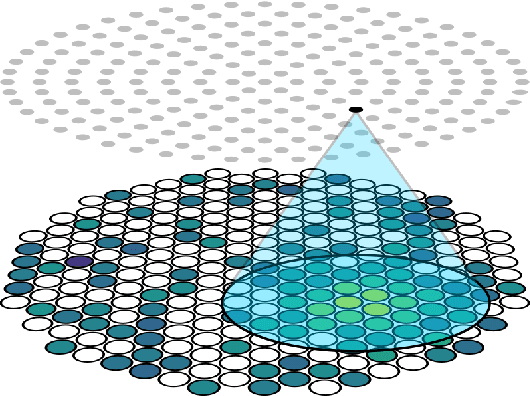
This work proposes a domain-informed neural network architecture for experimental particle physics, using particle interaction localization with the time-projection chamber (TPC) technology for dark matter research as an example application. A key feature of the signals generated within the TPC is that they allow localization of particle interactions through a process called reconstruction. While multilayer perceptrons (MLPs) have emerged as a leading contender for reconstruction in TPCs, such a black-box approach does not reflect prior knowledge of the underlying scientific processes. This paper looks anew at neural network-based interaction localization and encodes prior detector knowledge, in terms of both signal characteristics and detector geometry, into the feature encoding and the output layers of a multilayer neural network. The resulting Domain-informed Neural Network (DiNN limits the receptive fields of the neurons in the initial feature encoding layers in order to account for the spatially localized nature of the signals produced within the TPC. This aspect of the DiNN, which has similarities with the emerging area of graph neural networks in that the neurons in the initial layers only connect to a handful of neurons in their succeeding layer, significantly reduces the number of parameters in the network in comparison to an MLP. In addition, in order to account for the detector geometry, the output layers of the network are modified using two geometric transformations to ensure the DiNN produces localizations within the interior of the detector. The end result is a neural network architecture that has 60% fewer parameters than an MLP, but that still achieves similar localization performance and provides a path to future architectural developments with improved performance because of their ability to encode additional domain knowledge into the architecture.