Correction Filter for Single Image Super-Resolution: Robustifying Off-the-Shelf Deep Super-Resolvers

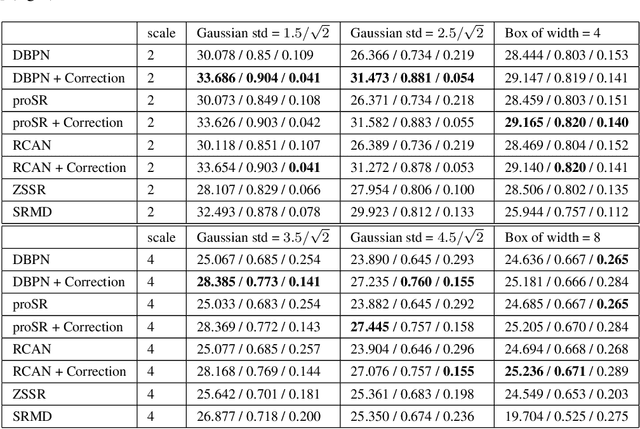
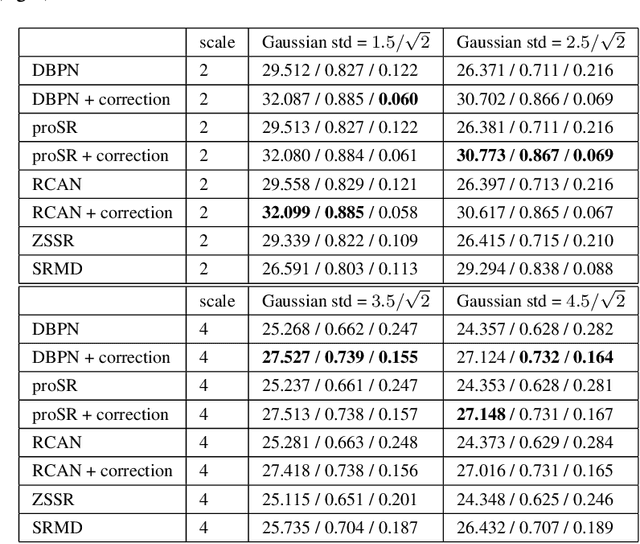
The single image super-resolution task is one of the most examined inverse problems in the past decade. In the recent years, Deep Neural Networks (DNNs) have shown superior performance over alternative methods when the acquisition process uses a fixed known downsampling kernel-typically a bicubic kernel. However, several recent works have shown that in practical scenarios, where the test data mismatch the training data (e.g. when the downsampling kernel is not the bicubic kernel or is not available at training), the leading DNN methods suffer from a huge performance drop. Inspired by the literature on generalized sampling, in this work we propose a method for improving the performance of DNNs that have been trained with a fixed kernel on observations acquired by other kernels. For a known kernel, we design a closed-form correction filter that modifies the low-resolution image to match one which is obtained by another kernel (e.g. bicubic), and thus improves the results of existing pre-trained DNNs. For an unknown kernel, we extend this idea and propose an algorithm for blind estimation of the required correction filter. We show that our approach outperforms other super-resolution methods, which are designed for general downsampling kernels.

Image-Adaptive GAN based Reconstruction

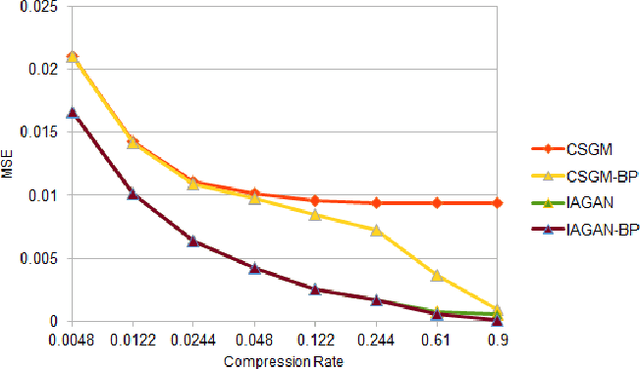
In the recent years, there has been a significant improvement in the quality of samples produced by (deep) generative models such as variational auto-encoders and generative adversarial networks. However, the representation capabilities of these methods still do not capture the full distribution for complex classes of images, such as human faces. This deficiency has been clearly observed in previous works that use pre-trained generative models to solve imaging inverse problems. In this paper, we suggest to mitigate the limited representation capabilities of generators by making them image-adaptive and enforcing compliance of the restoration with the observations via back-projections. We empirically demonstrate the advantages of our proposed approach for image super-resolution and compressed sensing