Building causation links in stochastic nonlinear systems from data

Causal relationships play a fundamental role in understanding the world around us. The ability to identify and understand cause-effect relationships is critical to making informed decisions, predicting outcomes, and developing effective strategies. However, deciphering causal relationships from observational data is a difficult task, as correlations alone may not provide definitive evidence of causality. In recent years, the field of machine learning (ML) has emerged as a powerful tool, offering new opportunities for uncovering hidden causal mechanisms and better understanding complex systems. In this work, we address the issue of detecting the intrinsic causal links of a large class of complex systems in the framework of the response theory in physics. We develop some theoretical ideas put forward by [1], and technically we use state-of-the-art ML techniques to build up models from data. We consider both linear stochastic and non-linear systems. Finally, we compute the asymptotic efficiency of the linear response based causal predictor in a case of large scale Markov process network of linear interactions.

Leveraging the structure of dynamical systems for data-driven modeling

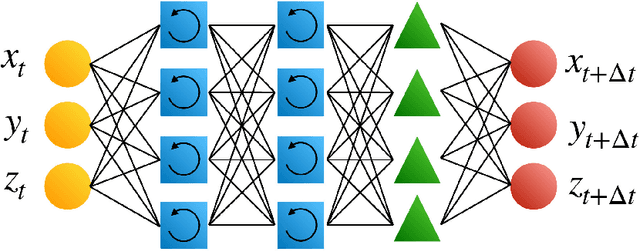
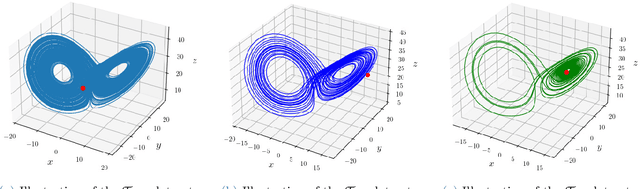
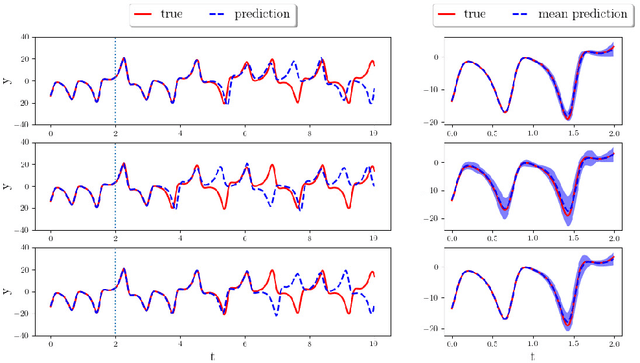
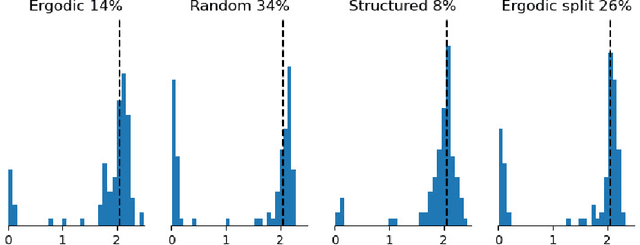
The reliable prediction of the temporal behavior of complex systems is required in numerous scientific fields. This strong interest is however hindered by modeling issues: often, the governing equations describing the physics of the system under consideration are not accessible or, when known, their solution might require a computational time incompatible with the prediction time constraints. Nowadays, approximating complex systems at hand in a generic functional format and informing it ex nihilo from available observations has become a common practice, as illustrated by the enormous amount of scientific work appeared in the last years. Numerous successful examples based on deep neural networks are already available, although generalizability of the models and margins of guarantee are often overlooked. Here, we consider Long-Short Term Memory neural networks and thoroughly investigate the impact of the training set and its structure on the quality of the long-term prediction. Leveraging ergodic theory, we analyze the amount of data sufficient for a priori guaranteeing a faithful model of the physical system. We show how an informed design of the training set, based on invariants of the system and the structure of the underlying attractor, significantly improves the resulting models, opening up avenues for research within the context of active learning. Further, the non-trivial effects of the memory initializations when relying on memory-capable models will be illustrated. Our findings provide evidence-based good-practice on the amount and the choice of data required for an effective data-driven modeling of any complex dynamical system.