SUS backprop: linear backpropagation algorithm for long inputs in transformers

It is straightforward to design an unbiased gradient estimator that stochastically cuts the backpropagation flow through any part of a computational graph. By cutting the parts that have little effect on the computation, one can potentially save a significant amount of back-propagation computation in exchange for a minimal increase in the stochastic gradient variance, in some situations. Such a situation occurs in the attention mechanism of the transformer architecture. For long sequences, attention becomes the limiting factor, as its compute requirements increase quadratically with sequence length $n$. At the same time, most attention weights become very small, as most attention heads tend to connect a given token with only a small fraction of other tokens in the sequence. These weights become promising targets for cutting backpropagation. We propose a simple probabilistic rule controlled by a single parameter $c$ that cuts backpropagation through most attention weights, leaving at most $c$ interactions per token per attention head. This brings a factor of $c/n$ reduction in the compute required for the attention backpropagation, turning it from quadratic $O(n^2)$ to linear complexity $O(nc)$. We have empirically verified that, for a typical transformer model, cutting $99\%$ of the attention gradient flow (i.e. choosing $c \sim 20-30$) results in relative gradient variance increase of only about $1\%$ for $n \sim 2000$, and it decreases with $n$. This approach is amenable to efficient sparse matrix implementation, thus being promising for making the cost of a backward pass negligible relative to the cost of a forward pass when training a transformer model on long sequences.

Energy-conserving intermittent-contact motion in complex models

Some mechanical systems, that are modeled to have inelastic collisions, nonetheless possess energy-conserving intermittent-contact solutions, known as collisionless solutions. Such a solution, representing a persistent hopping or walking across a level ground, may be important for understanding animal locomotion or for designing efficient walking machines. So far, collisionless motion has been analytically studied in simple two degrees of freedom (DOF) systems, or in a system that decouples into 2-DOF subsystems in the harmonic approximation. In this paper we extend the consideration to a N-DOF system, recovering the known solutions as a special N = 2 case of the general formulation. We show that in the harmonic approximation the collisionless solution is determined by the spectrum of the system. We formulate a solution existence condition, which requires the presence of at least one oscillating normal mode in the most constrained phase of the motion. An application of the developed general framework is illustrated by finding a collisionless solution for a rocking motion of a biped with an armed standing torso.

Configuration Path Control

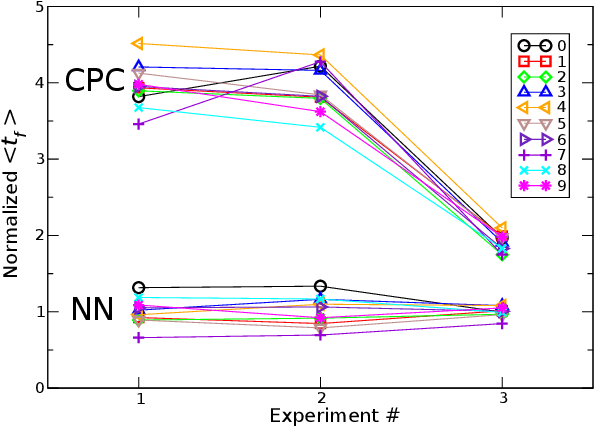
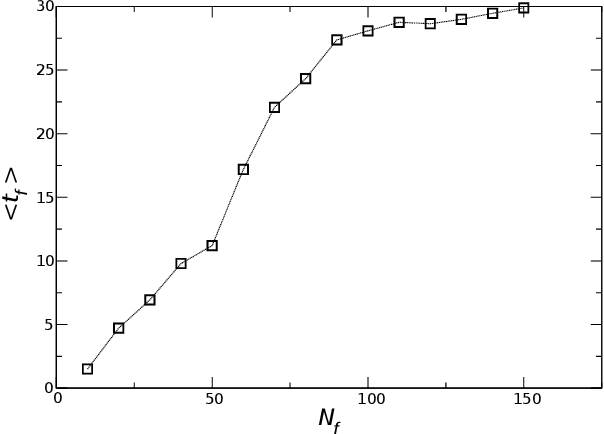
Reinforcement learning methods often produce brittle policies -- policies that perform well during training, but generalize poorly beyond their direct training experience, thus becoming unstable under small disturbances. To address this issue, we propose a method for stabilizing a control policy in the space of configuration paths. It is applied post-training and relies purely on the data produced during training, as well as on an instantaneous control-matrix estimation. The approach is evaluated empirically on a planar bipedal walker subjected to a variety of perturbations. The control policies obtained via reinforcement learning are compared against their stabilized counterparts. Across different experiments, we find two- to four-fold increase in stability, when measured in terms of the perturbation amplitudes. We also provide a zero-dynamics interpretation of our approach.

Three-dimensional bipedal model with zero-energy-cost walking

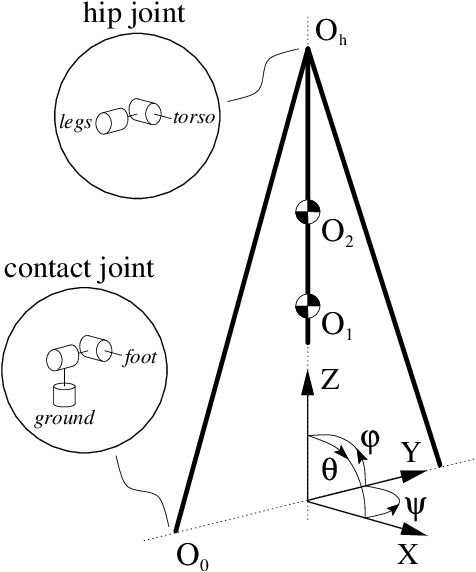
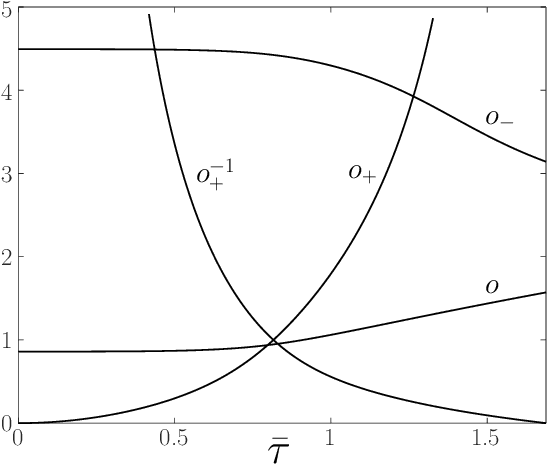
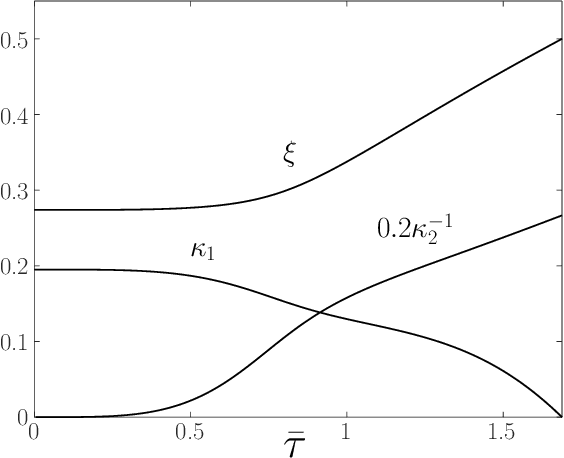
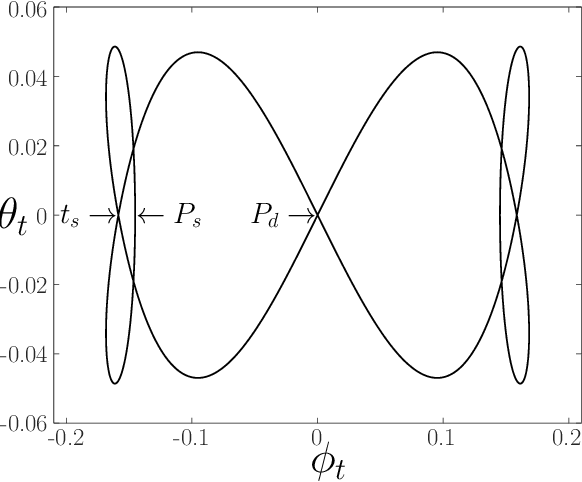
We study a three-dimensional articulated rigid-body biped model that possesses zero cost of transport walking gaits. Energy losses are avoided due to the complete elimination of the foot-ground collisions by the concerted oscillatory motion of the model's parts. The model consists of two parts connected via a universal joint. It does not rely on any geometry altering mechanisms, massless parts or springs. Despite the model's simplicity, its collisionless gaits feature walking with finite speed, foot clearance and ground friction. The collisionless spectrum can be studied analytically in the small movement limit, revealing infinitely many periodic modes. The modes differ in the number of sagittal and coronal plane oscillations at different stages of the walking cycle. We focus on the mode with the minimal number of such oscillations, presenting its complete analytical solution. We then numerically evolve it toward a general non-small movement solution. A general collisionless mode can be tuned by adjusting a single model parameter. Some of the presented results display a surprising degree of generality and universality.

Reward-estimation variance elimination in sequential decision processes

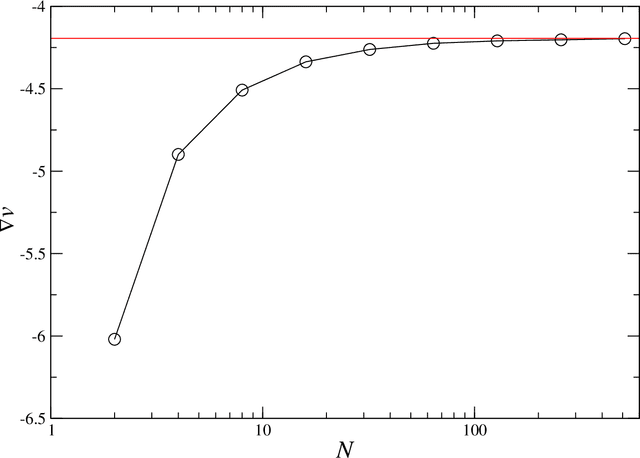
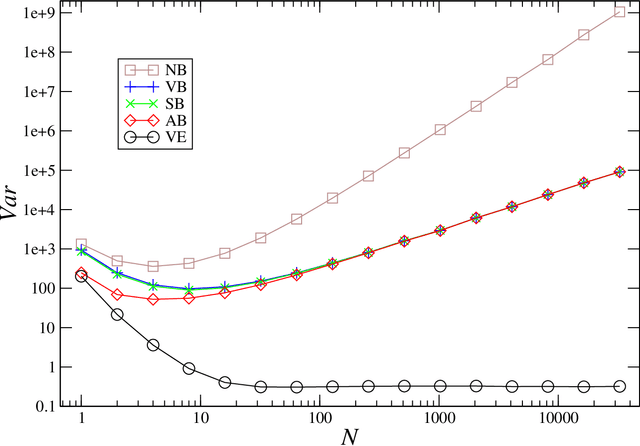
Policy gradient methods are very attractive in reinforcement learning due to their model-free nature and convergence guarantees. These methods, however, suffer from high variance in gradient estimation, resulting in poor sample efficiency. To mitigate this issue, a number of variance-reduction approaches have been proposed. Unfortunately, in the challenging problems with delayed rewards, these approaches either bring a relatively modest improvement or do reduce variance at expense of introducing a bias and undermining convergence. The unbiased methods of gradient estimation, in general, only partially reduce variance, without eliminating it completely even in the limit of exact knowledge of the value functions and problem dynamics, as one might have wished. In this work we propose an unbiased method that does completely eliminate variance under some, commonly encountered, conditions. Of practical interest is the limit of deterministic dynamics and small policy stochasticity. In the case of a quadratic value function, as in linear quadratic Gaussian models, the policy randomness need not be small. We use such a model to analyze performance of the proposed variance-elimination approach and compare it with standard variance-reduction methods. The core idea behind the approach is to use control variates at all future times down the trajectory. We present both a model-based and model-free formulations.

Learning image transformations without training examples

The use of image transformations is essential for efficient modeling and learning of visual data. But the class of relevant transformations is large: affine transformations, projective transformations, elastic deformations, ... the list goes on. Therefore, learning these transformations, rather than hand coding them, is of great conceptual interest. To the best of our knowledge, all the related work so far has been concerned with either supervised or weakly supervised learning (from correlated sequences, video streams, or image-transform pairs). In this paper, on the contrary, we present a simple method for learning affine and elastic transformations when no examples of these transformations are explicitly given, and no prior knowledge of space (such as ordering of pixels) is included either. The system has only access to a moderately large database of natural images arranged in no particular order.