Federated Binary Matrix Factorization using Proximal Optimization

Identifying informative components in binary data is an essential task in many research areas, including life sciences, social sciences, and recommendation systems. Boolean matrix factorization (BMF) is a family of methods that performs this task by efficiently factorizing the data. In real-world settings, the data is often distributed across stakeholders and required to stay private, prohibiting the straightforward application of BMF. To adapt BMF to this context, we approach the problem from a federated-learning perspective, while building on a state-of-the-art continuous binary matrix factorization relaxation to BMF that enables efficient gradient-based optimization. We propose to only share the relaxed component matrices, which are aggregated centrally using a proximal operator that regularizes for binary outcomes. We show the convergence of our federated proximal gradient descent algorithm and provide differential privacy guarantees. Our extensive empirical evaluation demonstrates that our algorithm outperforms, in terms of quality and efficacy, federation schemes of state-of-the-art BMF methods on a diverse set of real-world and synthetic data.

Efficiently Factorizing Boolean Matrices using Proximal Gradient Descent

Addressing the interpretability problem of NMF on Boolean data, Boolean Matrix Factorization (BMF) uses Boolean algebra to decompose the input into low-rank Boolean factor matrices. These matrices are highly interpretable and very useful in practice, but they come at the high computational cost of solving an NP-hard combinatorial optimization problem. To reduce the computational burden, we propose to relax BMF continuously using a novel elastic-binary regularizer, from which we derive a proximal gradient algorithm. Through an extensive set of experiments, we demonstrate that our method works well in practice: On synthetic data, we show that it converges quickly, recovers the ground truth precisely, and estimates the simulated rank exactly. On real-world data, we improve upon the state of the art in recall, loss, and runtime, and a case study from the medical domain confirms that our results are easily interpretable and semantically meaningful.

Differentially Describing Groups of Graphs

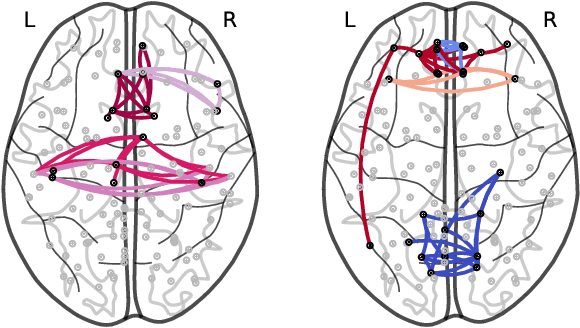
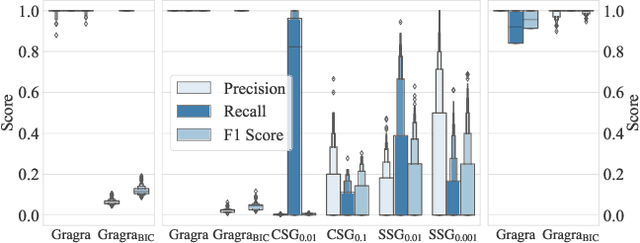
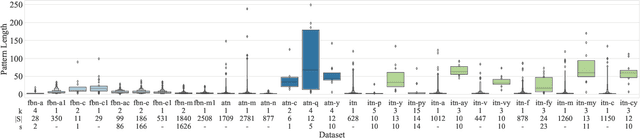
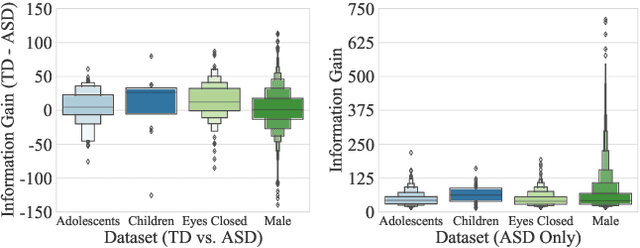
How does neural connectivity in autistic children differ from neural connectivity in healthy children or autistic youths? What patterns in global trade networks are shared across classes of goods, and how do these patterns change over time? Answering questions like these requires us to differentially describe groups of graphs: Given a set of graphs and a partition of these graphs into groups, discover what graphs in one group have in common, how they systematically differ from graphs in other groups, and how multiple groups of graphs are related. We refer to this task as graph group analysis, which seeks to describe similarities and differences between graph groups by means of statistically significant subgraphs. To perform graph group analysis, we introduce Gragra, which uses maximum entropy modeling to identify a non-redundant set of subgraphs with statistically significant associations to one or more graph groups. Through an extensive set of experiments on a wide range of synthetic and real-world graph groups, we confirm that Gragra works well in practice.