Multilevel and Sequential Monte Carlo for Training-Free Diffusion Guidance

We address the problem of accurate, training-free guidance for conditional generation in trained diffusion models. Existing methods typically rely on point-estimates to approximate the posterior score, often resulting in biased approximations that fail to capture multimodality inherent to the reverse process of diffusion models. We propose a sequential Monte Carlo (SMC) framework that constructs an unbiased estimator of $p_θ(y|x_t)$ by integrating over the full denoising distribution via Monte Carlo approximation. To ensure computational tractability, we incorporate variance-reduction schemes based on Multi-Level Monte Carlo (MLMC). Our approach achieves new state-of-the-art results for training-free guidance on CIFAR-10 class-conditional generation, achieving $95.6\%$ accuracy with $3\times$ lower cost-per-success than baselines. On ImageNet, our algorithm achieves $1.5\times$ cost-per-success advantage over existing methods.

Finite Sample Complexity of Sequential Monte Carlo Estimators on Multimodal Target Distributions

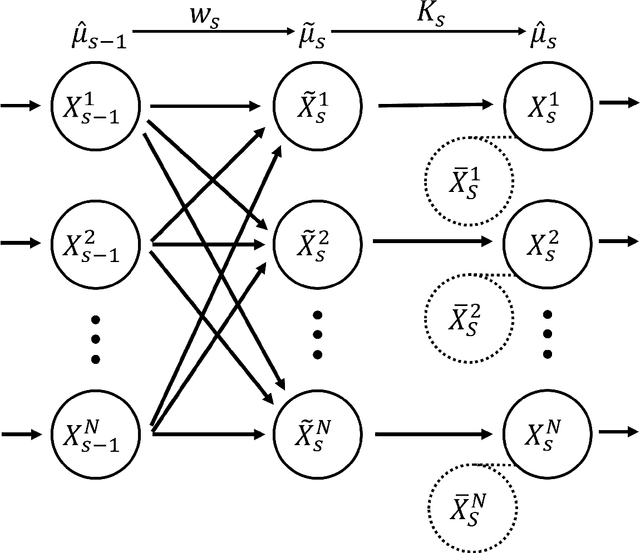
We prove finite sample complexities for sequential Monte Carlo (SMC) algorithms which require only local mixing times of the associated Markov kernels. Our bounds are particularly useful when the target distribution is multimodal and global mixing of the Markov kernel is slow; in such cases our approach establishes the benefits of SMC over the corresponding Markov chain Monte Carlo (MCMC) estimator. The lack of global mixing is addressed by sequentially controlling the bias introduced by SMC resampling procedures. We apply these results to obtain complexity bounds for approximating expectations under mixtures of log-concave distributions and show that SMC provides a fully polynomial time randomized approximation scheme for some difficult multimodal problems where the corresponding Markov chain sampler is exponentially slow. Finally, we compare the bounds obtained by our approach to existing bounds for tempered Markov chains on the same problems.