Every Bit Counts: A Theoretical Study of Precision-Expressivity Tradeoffs in Quantized Transformers

Quantization reduces the numerical precision of Transformer computations and is widely used to accelerate inference, yet its effect on expressivity remains poorly characterized. We demonstrate a fine-grained theoretical tradeoff between expressivity and precision: For every p we exhibit a function Γ, inspired by the equality function, and prove that a one-layer softmax Transformer can compute Γ, with p bits of precision, but not with p-1 bits of precision. This result concretely explains the widely observed phenomenon of empirical loss of expressivity when quantization is used. Practically, it suggests that tasks requiring equality-like comparisons (exact match, membership, etc.) are especially sensitive to quantization. Dropping even one bit can cross a threshold where the model cannot represent the needed comparison reliably. Thus, it paves the way for developing heuristics that will help practitioners choose how much quantization is possible: the precision should be chosen as a function of the length of equality to be checked for the specific task. Our proofs combine explicit finite-precision Transformer constructions with communication-complexity lower bounds, yielding a tight "one-bit" threshold.

Poly-attention: a general scheme for higher-order self-attention

The self-attention mechanism, at the heart of the Transformer model, is able to effectively model pairwise interactions between tokens. However, numerous recent works have shown that it is unable to perform basic tasks involving detecting triples of correlated tokens, or compositional tasks where multiple input tokens need to be referenced to generate a result. Some higher-dimensional alternatives to self-attention have been proposed to address this, including higher-order attention and Strassen attention, which can perform some of these polyadic tasks in exchange for slower, superquadratic running times. In this work, we define a vast class of generalizations of self-attention, which we call poly-attention mechanisms. Our mechanisms can incorporate arbitrary higher-order (tensor) computations as well as arbitrary relationship structures between the input tokens, and they include the aforementioned alternatives as special cases. We then systematically study their computational complexity and representational strength, including giving new algorithms and matching complexity-theoretic lower bounds on the time complexity of computing the attention matrix exactly as well as approximately, and tightly determining which polyadic tasks they can each perform. Our results give interesting trade-offs between different desiderata for these mechanisms, including a tight relationship between how expressive a mechanism is, and how large the coefficients in the model may be so that the mechanism can be approximated in almost-linear time. Notably, we give a new attention mechanism which can be computed exactly in quadratic time, and which can perform function composition for any fixed number of functions. Prior mechanisms, even for just composing two functions, could only be computed in superquadratic time, and our new lower bounds show that faster algorithms for them are not possible.

Graphon Estimation from Partially Observed Network Data

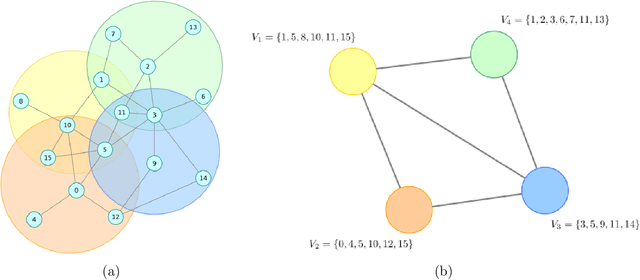
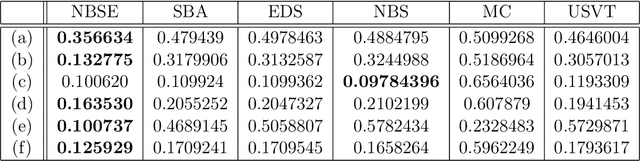
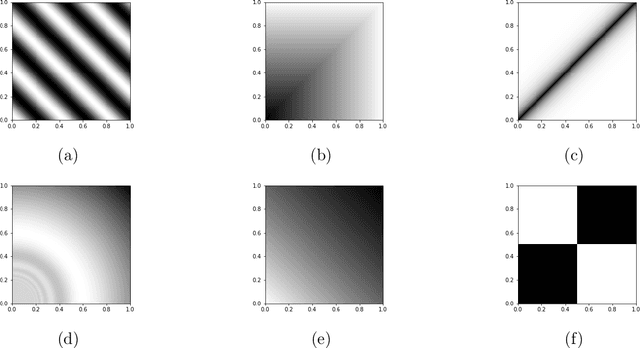
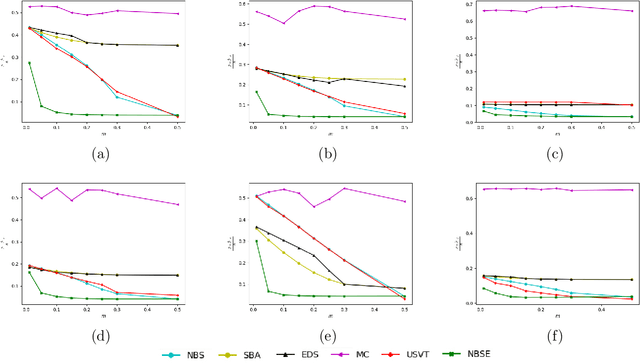
We consider estimating the edge-probability matrix of a network generated from a graphon model when the full network is not observed---only some overlapping subgraphs are. We extend the neighbourhood smoothing (NBS) algorithm of Zhang et al. (2017) to this missing-data set-up and show experimentally that, for a wide range of graphons, the extended NBS algorithm achieves significantly smaller error rates than standard graphon estimation algorithms such as vanilla neighbourhood smoothing (NBS), universal singular value thresholding (USVT), blockmodel approximation, matrix completion, etc. We also show that the extended NBS algorithm is much more robust to missing data.