Predictive Scale-Bridging Simulations through Active Learning

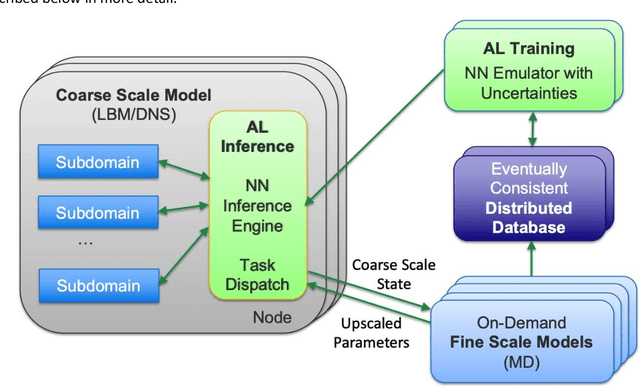
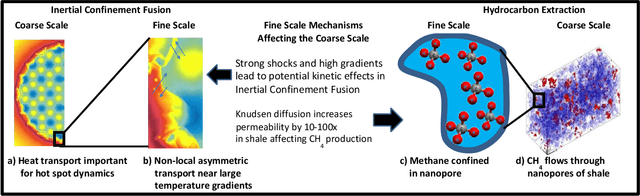
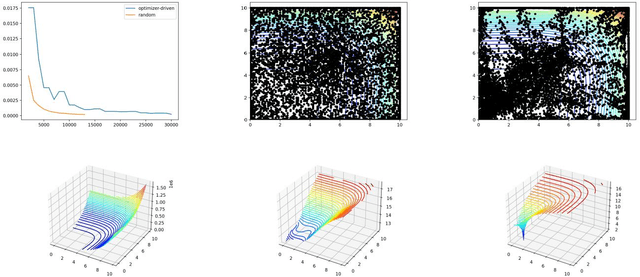
Throughout computational science, there is a growing need to utilize the continual improvements in raw computational horsepower to achieve greater physical fidelity through scale-bridging over brute-force increases in the number of mesh elements. For instance, quantitative predictions of transport in nanoporous media, critical to hydrocarbon extraction from tight shale formations, are impossible without accounting for molecular-level interactions. Similarly, inertial confinement fusion simulations rely on numerical diffusion to simulate molecular effects such as non-local transport and mixing without truly accounting for molecular interactions. With these two disparate applications in mind, we develop a novel capability which uses an active learning approach to optimize the use of local fine-scale simulations for informing coarse-scale hydrodynamics. Our approach addresses three challenges: forecasting continuum coarse-scale trajectory to speculatively execute new fine-scale molecular dynamics calculations, dynamically updating coarse-scale from fine-scale calculations, and quantifying uncertainty in neural network models.

AdjointNet: Constraining machine learning models with physics-based codes

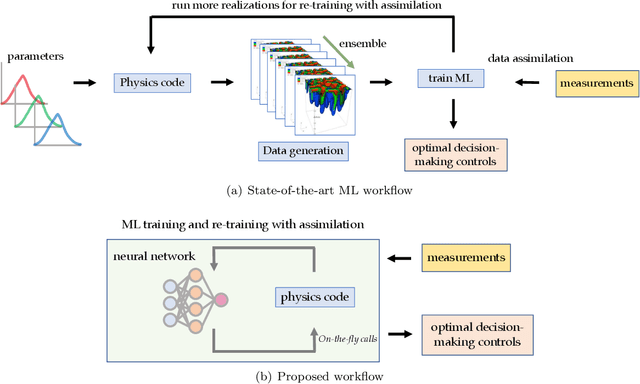
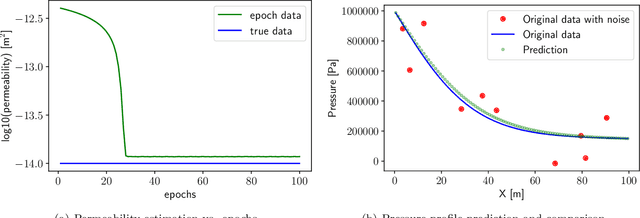
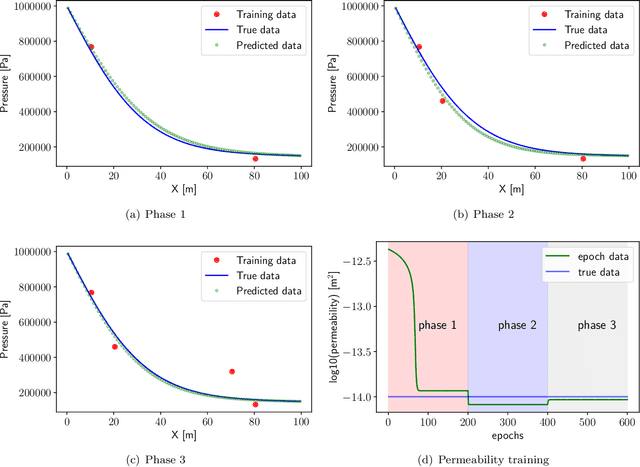
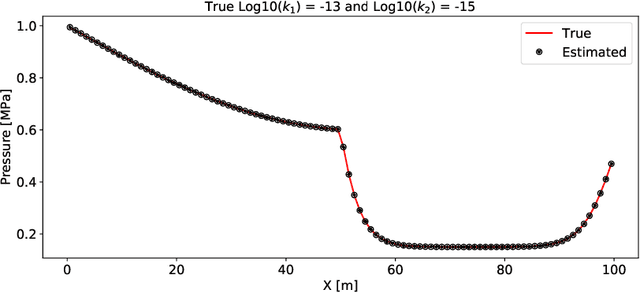
Physics-informed Machine Learning has recently become attractive for learning physical parameters and features from simulation and observation data. However, most existing methods do not ensure that the physics, such as balance laws (e.g., mass, momentum, energy conservation), are constrained. Some recent works (e.g., physics-informed neural networks) softly enforce physics constraints by including partial differential equation (PDE)-based loss functions but need re-discretization of the PDEs using auto-differentiation. Training these neural nets on observational data showed that one could solve forward and inverse problems in one shot. They evaluate the state variables and the parameters in a PDE. This re-discretization of PDEs is not necessarily an attractive option for domain scientists that work with physics-based codes that have been developed for decades with sophisticated discretization techniques to solve complex process models and advanced equations of state. This paper proposes a physics constrained machine learning framework, AdjointNet, allowing domain scientists to embed their physics code in neural network training workflows. This embedding ensures that physics is constrained everywhere in the domain. Additionally, the mathematical properties such as consistency, stability, and convergence vital to the numerical solution of a PDE are still satisfied. We show that the proposed AdjointNet framework can be used for parameter estimation (and uncertainty quantification by extension) and experimental design using active learning. The applicability of our framework is demonstrated for four flow cases. Results show that AdjointNet-based inversion can estimate process model parameters with reasonable accuracy. These examples demonstrate the applicability of using existing software with no changes in source code to perform accurate and reliable inversion of model parameters.