Bayesian Optimistic Optimisation with Exponentially Decaying Regret

Bayesian optimisation (BO) is a well-known efficient algorithm for finding the global optimum of expensive, black-box functions. The current practical BO algorithms have regret bounds ranging from $\mathcal{O}(\frac{logN}{\sqrt{N}})$ to $\mathcal O(e^{-\sqrt{N}})$, where $N$ is the number of evaluations. This paper explores the possibility of improving the regret bound in the noiseless setting by intertwining concepts from BO and tree-based optimistic optimisation which are based on partitioning the search space. We propose the BOO algorithm, a first practical approach which can achieve an exponential regret bound with order $\mathcal O(N^{-\sqrt{N}})$ under the assumption that the objective function is sampled from a Gaussian process with a Mat\'ern kernel with smoothness parameter $\nu > 4 +\frac{D}{2}$, where $D$ is the number of dimensions. We perform experiments on optimisation of various synthetic functions and machine learning hyperparameter tuning tasks and show that our algorithm outperforms baselines.

Intuitive Physics Guided Exploration for Sample Efficient Sim2real Transfer

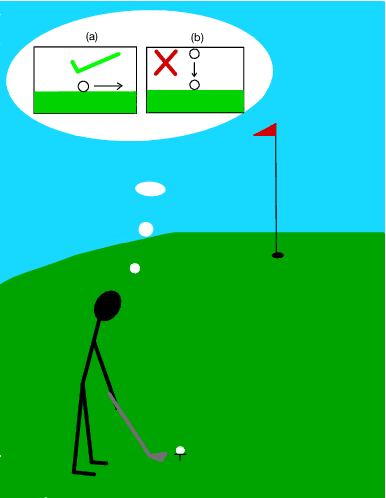
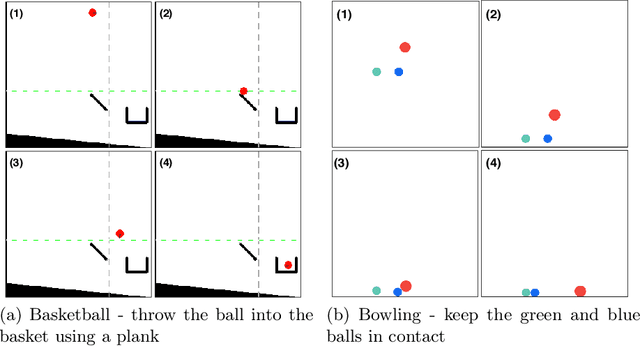
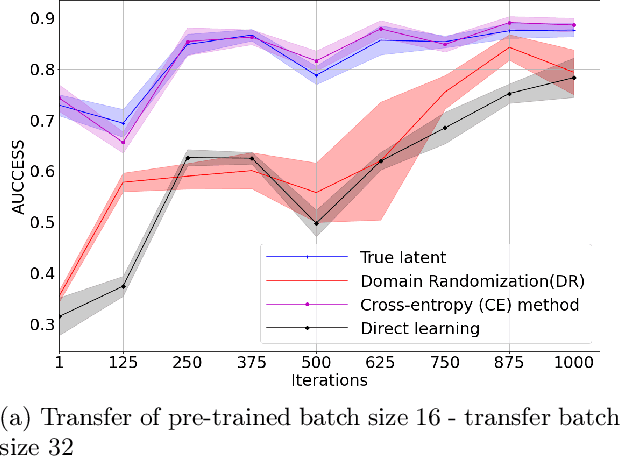
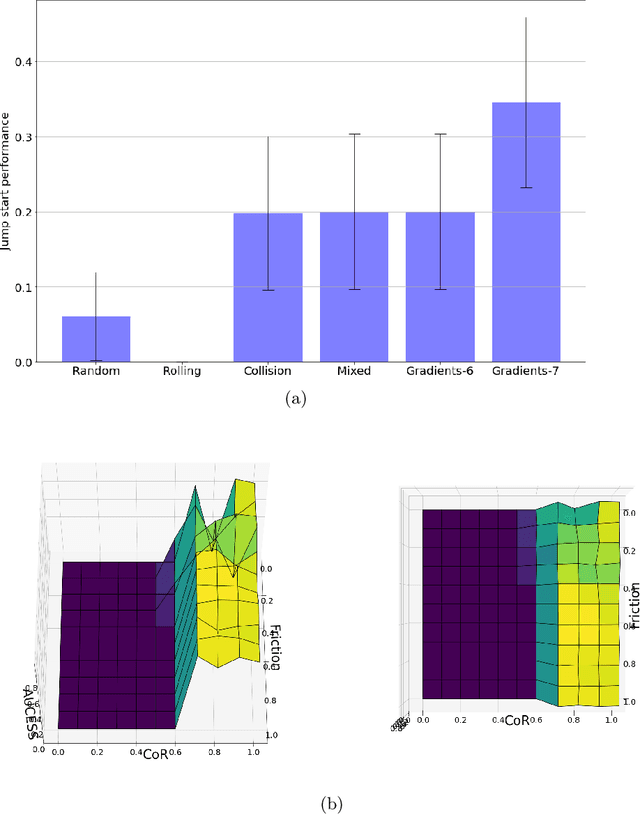
Physics-based reinforcement learning tasks can benefit from simplified physics simulators as they potentially allow near-optimal policies to be learned in simulation. However, such simulators require the latent factors (e.g. mass, friction coefficient etc.) of the associated objects and other environment-specific factors (e.g. wind speed, air density etc.) to be accurately specified, without which, it could take considerable additional learning effort to adapt the learned simulation policy to the real environment. As such a complete specification can be impractical, in this paper, we instead, focus on learning task-specific estimates of latent factors which allow the approximation of real world trajectories in an ideal simulation environment. Specifically, we propose two new concepts: a) action grouping - the idea that certain types of actions are closely associated with the estimation of certain latent factors, and; b) partial grounding - the idea that simulation of task-specific dynamics may not need precise estimation of all the latent factors. We first introduce intuitive action groupings based on human physics knowledge and experience, which is then used to design novel strategies for interacting with the real environment. Next, we describe how prior knowledge of a task in a given environment can be used to extract the relative importance of different latent factors, and how this can be used to inform partial grounding, which enables efficient learning of the task in any arbitrary environment. We demonstrate our approach in a range of physics based tasks, and show that it achieves superior performance relative to other baselines, using only a limited number of real-world interactions.

ALT-MAS: A Data-Efficient Framework for Active Testing of Machine Learning Algorithms

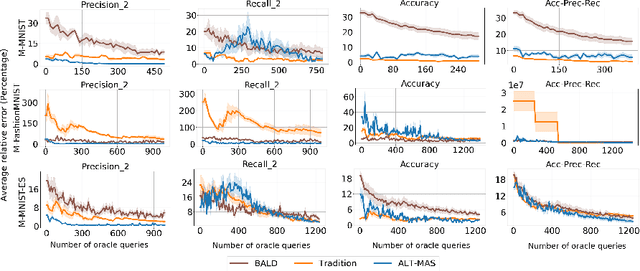
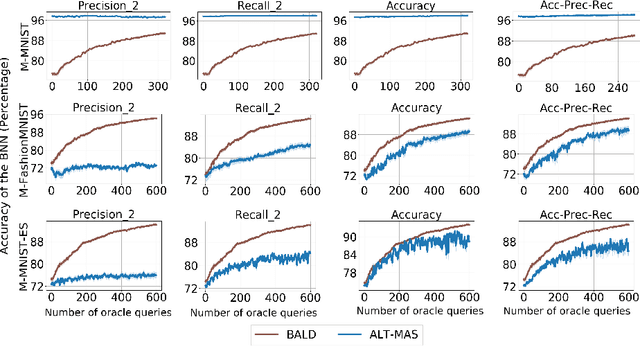
Machine learning models are being used extensively in many important areas, but there is no guarantee a model will always perform well or as its developers intended. Understanding the correctness of a model is crucial to prevent potential failures that may have significant detrimental impact in critical application areas. In this paper, we propose a novel framework to efficiently test a machine learning model using only a small amount of labeled test data. The idea is to estimate the metrics of interest for a model-under-test using Bayesian neural network (BNN). We develop a novel data augmentation method helping to train the BNN to achieve high accuracy. We also devise a theoretic information based sampling strategy to sample data points so as to achieve accurate estimations for the metrics of interest. Finally, we conduct an extensive set of experiments to test various machine learning models for different types of metrics. Our experiments show that the metrics estimations by our method are significantly better than existing baselines.

High Dimensional Level Set Estimation with Bayesian Neural Network

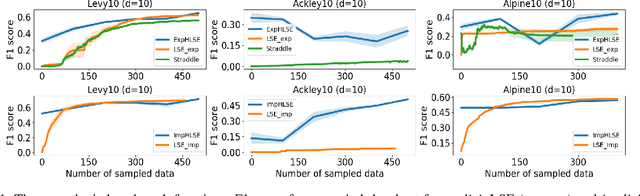
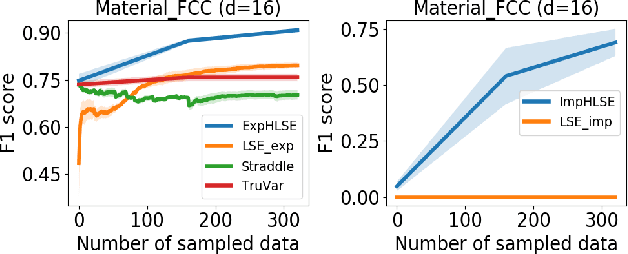
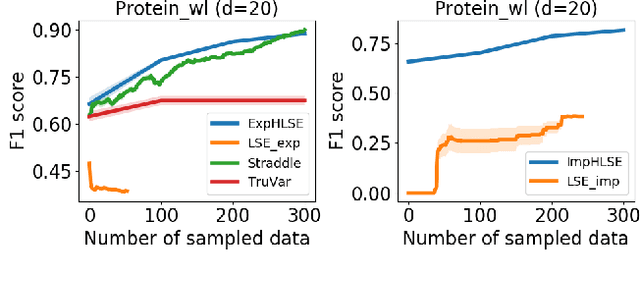
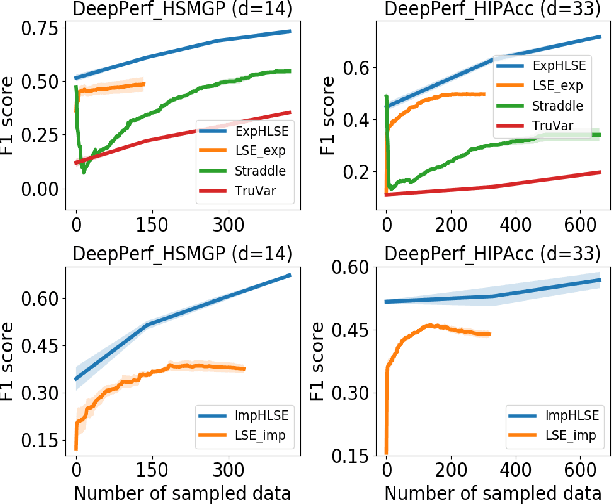
Level Set Estimation (LSE) is an important problem with applications in various fields such as material design, biotechnology, machine operational testing, etc. Existing techniques suffer from the scalability issue, that is, these methods do not work well with high dimensional inputs. This paper proposes novel methods to solve the high dimensional LSE problems using Bayesian Neural Networks. In particular, we consider two types of LSE problems: (1) \textit{explicit} LSE problem where the threshold level is a fixed user-specified value, and, (2) \textit{implicit} LSE problem where the threshold level is defined as a percentage of the (unknown) maximum of the objective function. For each problem, we derive the corresponding theoretic information based acquisition function to sample the data points so as to maximally increase the level set accuracy. Furthermore, we also analyse the theoretical time complexity of our proposed acquisition functions, and suggest a practical methodology to efficiently tune the network hyper-parameters to achieve high model accuracy. Numerical experiments on both synthetic and real-world datasets show that our proposed method can achieve better results compared to existing state-of-the-art approaches.

Logically Consistent Loss for Visual Question Answering

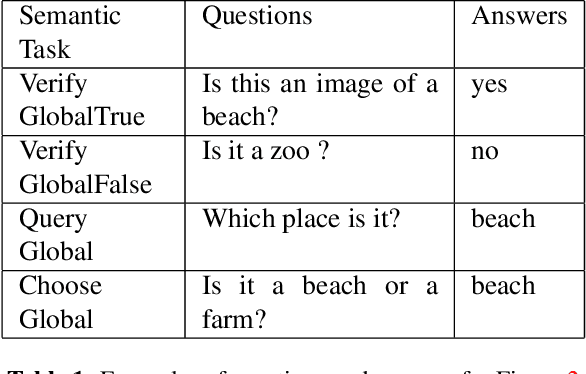
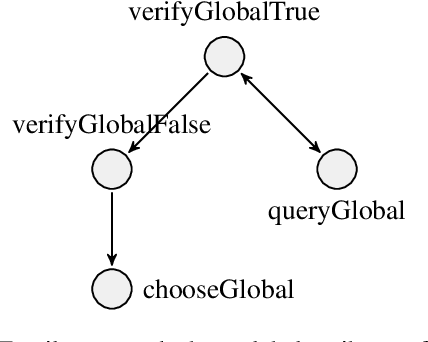
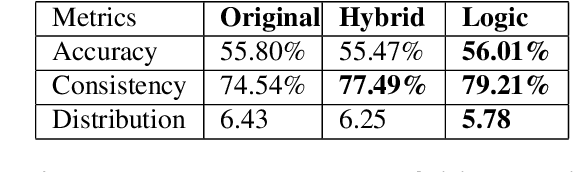
Given an image, a back-ground knowledge, and a set of questions about an object, human learners answer the questions very consistently regardless of question forms and semantic tasks. The current advancement in neural-network based Visual Question Answering (VQA), despite their impressive performance, cannot ensure such consistency due to identically distribution (i.i.d.) assumption. We propose a new model-agnostic logic constraint to tackle this issue by formulating a logically consistent loss in the multi-task learning framework as well as a data organisation called family-batch and hybrid-batch. To demonstrate usefulness of this proposal, we train and evaluate MAC-net based VQA machines with and without the proposed logically consistent loss and the proposed data organization. The experiments confirm that the proposed loss formulae and introduction of hybrid-batch leads to more consistency as well as better performance. Though the proposed approach is tested with MAC-net, it can be utilised in any other QA methods whenever the logical consistency between answers exist.

Unsupervised Anomaly Detection on Temporal Multiway Data

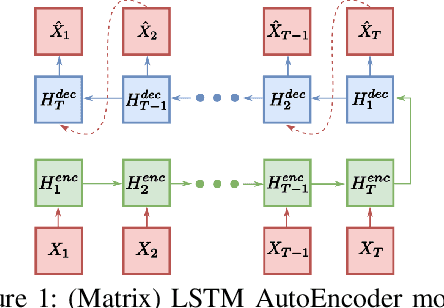
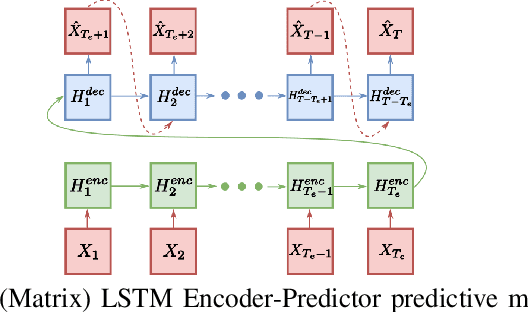
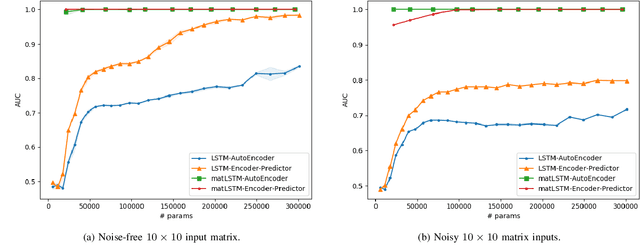
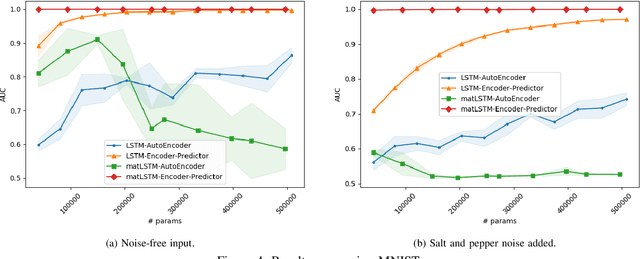
Temporal anomaly detection looks for irregularities over space-time. Unsupervised temporal models employed thus far typically work on sequences of feature vectors, and much less on temporal multiway data. We focus our investigation on two-way data, in which a data matrix is observed at each time step. Leveraging recent advances in matrix-native recurrent neural networks, we investigated strategies for data arrangement and unsupervised training for temporal multiway anomaly detection. These include compressing-decompressing, encoding-predicting, and temporal data differencing. We conducted a comprehensive suite of experiments to evaluate model behaviors under various settings on synthetic data, moving digits, and ECG recordings. We found interesting phenomena not previously reported. These include the capacity of the compact matrix LSTM to compress noisy data near perfectly, making the strategy of compressing-decompressing data ill-suited for anomaly detection under the noise. Also, long sequence of vectors can be addressed directly by matrix models that allow very long context and multiple step prediction. Overall, the encoding-predicting strategy works very well for the matrix LSTMs in the conducted experiments, thanks to its compactness and better fit to the data dynamics.

Sub-linear Regret Bounds for Bayesian Optimisation in Unknown Search Spaces

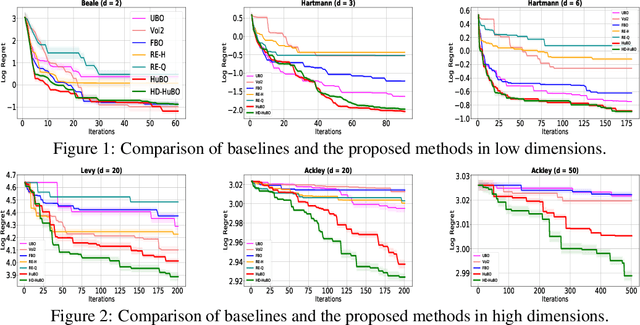
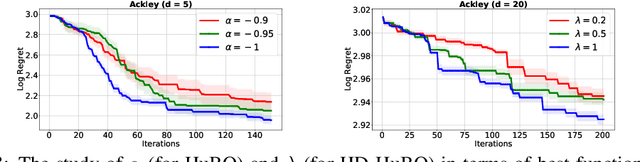
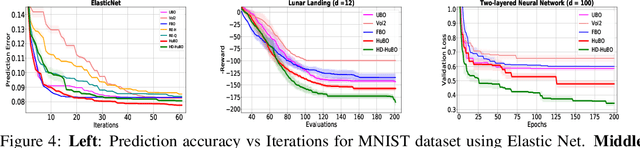
Bayesian optimisation is a popular method for efficient optimisation of expensive black-box functions. Traditionally, BO assumes that the search space is known. However, in many problems, this assumption does not hold. To this end, we propose a novel BO algorithm which expands (and shifts) the search space over iterations based on controlling the expansion rate thought a hyperharmonic series. Further, we propose another variant of our algorithm that scales to high dimensions. We show theoretically that for both our algorithms, the cumulative regret grows at sub-linear rates. Our experiments with synthetic and real-world optimisation tasks demonstrate the superiority of our algorithms over the current state-of-the-art methods for Bayesian optimisation in unknown search space.

Sequential Subspace Search for Functional Bayesian Optimization Incorporating Experimenter Intuition

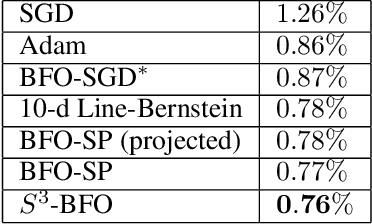
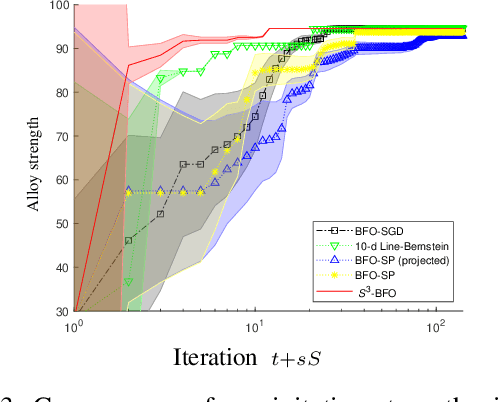
We propose an algorithm for Bayesian functional optimisation - that is, finding the function to optimise a process - guided by experimenter beliefs and intuitions regarding the expected characteristics (length-scale, smoothness, cyclicity etc.) of the optimal solution encoded into the covariance function of a Gaussian Process. Our algorithm generates a sequence of finite-dimensional random subspaces of functional space spanned by a set of draws from the experimenter's Gaussian Process. Standard Bayesian optimisation is applied on each subspace, and the best solution found used as a starting point (origin) for the next subspace. Using the concept of effective dimensionality, we analyse the convergence of our algorithm and provide a regret bound to show that our algorithm converges in sub-linear time provided a finite effective dimension exists. We test our algorithm in simulated and real-world experiments, namely blind function matching, finding the optimal precipitation-strengthening function for an aluminium alloy, and learning rate schedule optimisation for deep networks.

Bayesian Optimization with Missing Inputs

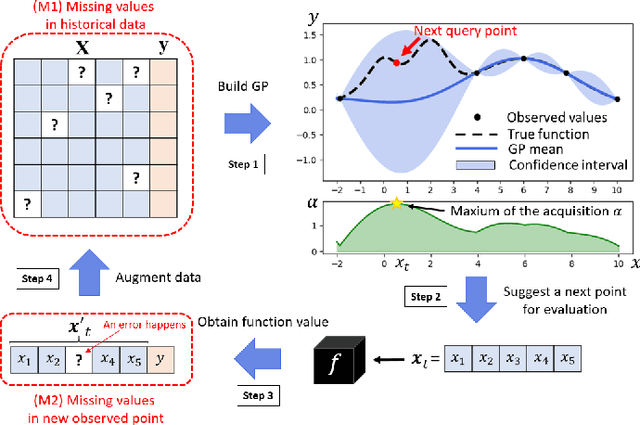
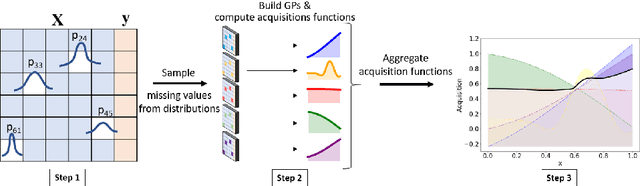
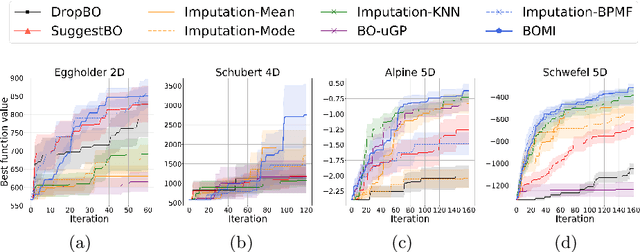
Bayesian optimization (BO) is an efficient method for optimizing expensive black-box functions. In real-world applications, BO often faces a major problem of missing values in inputs. The missing inputs can happen in two cases. First, the historical data for training BO often contain missing values. Second, when performing the function evaluation (e.g. computing alloy strength in a heat treatment process), errors may occur (e.g. a thermostat stops working) leading to an erroneous situation where the function is computed at a random unknown value instead of the suggested value. To deal with this problem, a common approach just simply skips data points where missing values happen. Clearly, this naive method cannot utilize data efficiently and often leads to poor performance. In this paper, we propose a novel BO method to handle missing inputs. We first find a probability distribution of each missing value so that we can impute the missing value by drawing a sample from its distribution. We then develop a new acquisition function based on the well-known Upper Confidence Bound (UCB) acquisition function, which considers the uncertainty of imputed values when suggesting the next point for function evaluation. We conduct comprehensive experiments on both synthetic and real-world applications to show the usefulness of our method.

DeepCoDA: personalized interpretability for compositional health data

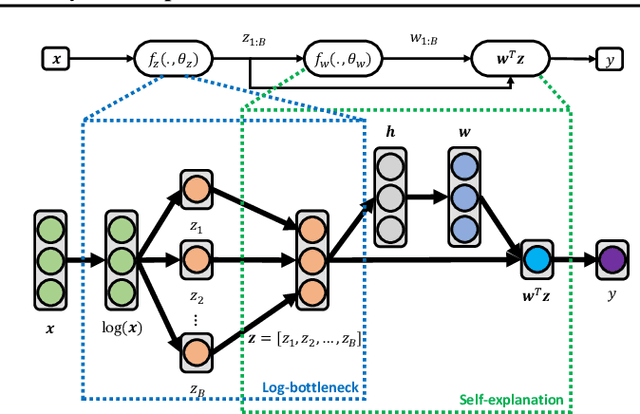
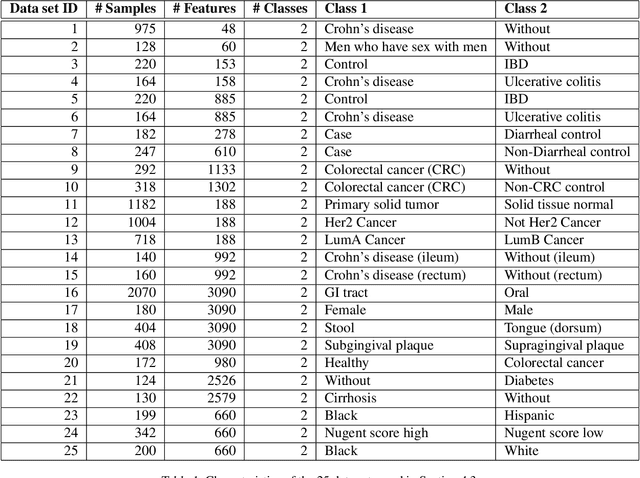
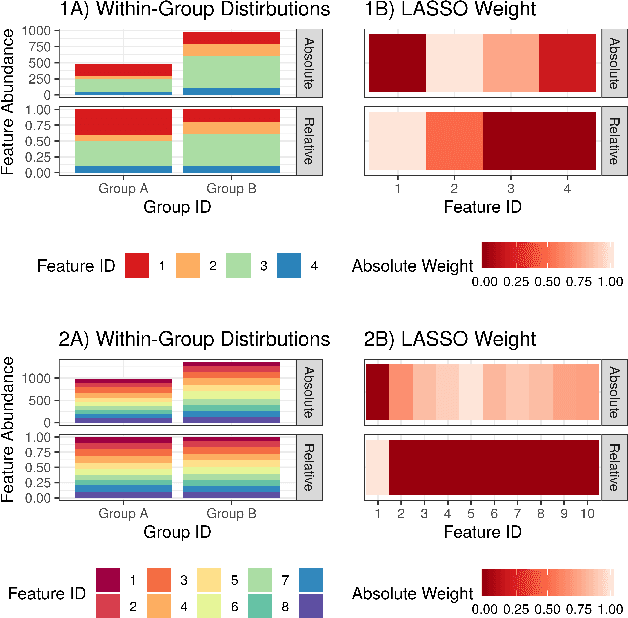
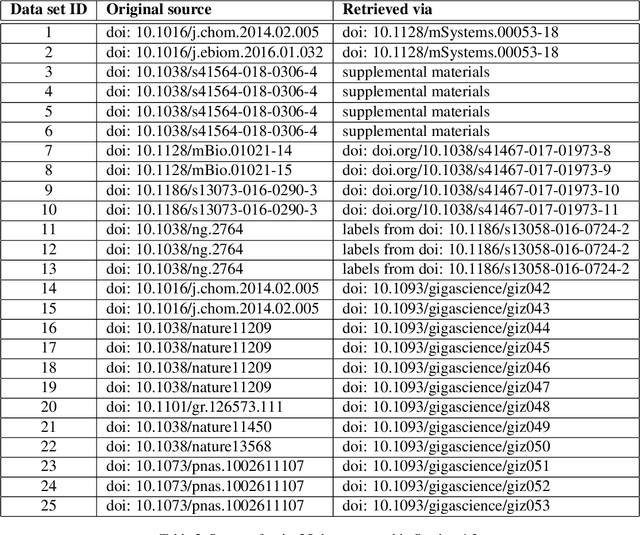
Interpretability allows the domain-expert to directly evaluate the model's relevance and reliability, a practice that offers assurance and builds trust. In the healthcare setting, interpretable models should implicate relevant biological mechanisms independent of technical factors like data pre-processing. We define personalized interpretability as a measure of sample-specific feature attribution, and view it as a minimum requirement for a precision health model to justify its conclusions. Some health data, especially those generated by high-throughput sequencing experiments, have nuances that compromise precision health models and their interpretation. These data are compositional, meaning that each feature is conditionally dependent on all other features. We propose the Deep Compositional Data Analysis (DeepCoDA) framework to extend precision health modelling to high-dimensional compositional data, and to provide personalized interpretability through patient-specific weights. Our architecture maintains state-of-the-art performance across 25 real-world data sets, all while producing interpretations that are both personalized and fully coherent for compositional data.