MRCpy: A Library for Minimax Risk Classifiers

Existing libraries for supervised classification implement techniques that are based on empirical risk minimization and utilize surrogate losses. We present MRCpy library that implements minimax risk classifiers (MRCs) that are based on robust risk minimization and can utilize 0-1-loss. Such techniques give rise to a manifold of classification methods that can provide tight bounds on the expected loss. MRCpy provides a unified interface for different variants of MRCs and follows the standards of popular Python libraries. The presented library also provides implementation for popular techniques that can be seen as MRCs such as L1-regularized logistic regression, zero-one adversarial, and maximum entropy machines. In addition, MRCpy implements recent feature mappings such as Fourier, ReLU, and threshold features. The library is designed with an object-oriented approach that facilitates collaborators and users.

Probabilistic Load Forecasting Based on Adaptive Online Learning

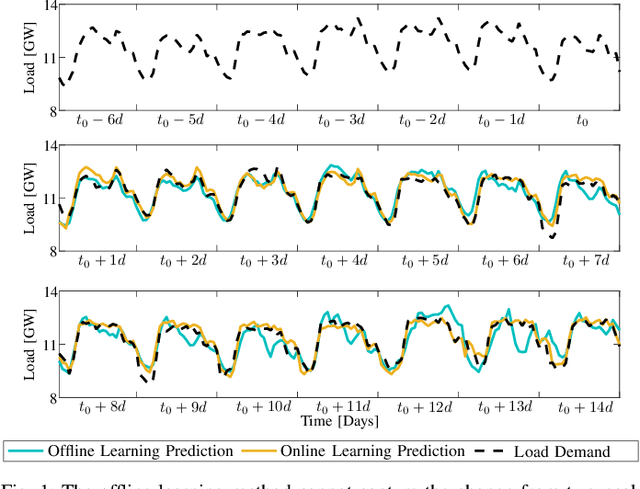
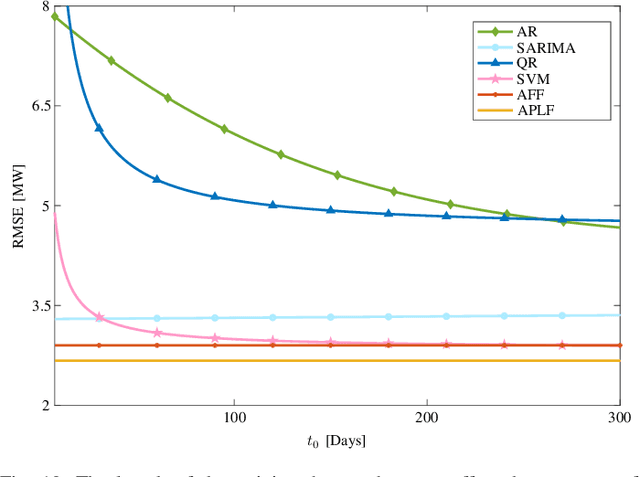
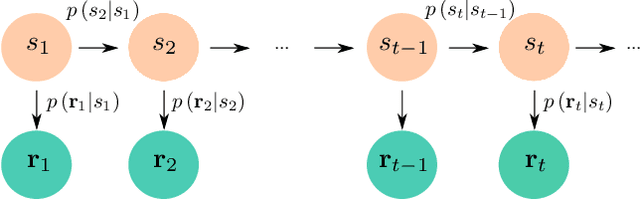
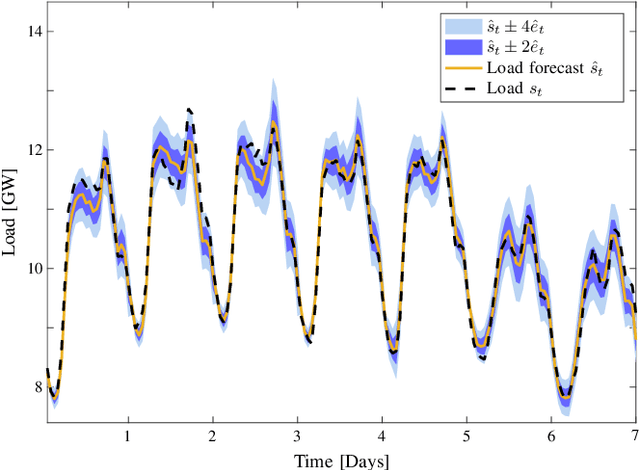
Load forecasting is crucial for multiple energy management tasks such as scheduling generation capacity, planning supply and demand, and minimizing energy trade costs. Such relevance has increased even more in recent years due to the integration of renewable energies, electric cars, and microgrids. Conventional load forecasting techniques obtain single-value load forecasts by exploiting consumption patterns of past load demand. However, such techniques cannot assess intrinsic uncertainties in load demand, and cannot capture dynamic changes in consumption patterns. To address these problems, this paper presents a method for probabilistic load forecasting based on the adaptive online learning of hidden Markov models. We propose learning and forecasting techniques with theoretical guarantees, and experimentally assess their performance in multiple scenarios. In particular, we develop adaptive online learning techniques that update model parameters recursively, and sequential prediction techniques that obtain probabilistic forecasts using the most recent parameters. The performance of the method is evaluated using multiple datasets corresponding with regions that have different sizes and display assorted time-varying consumption patterns. The results show that the proposed method can significantly improve the performance of existing techniques for a wide range of scenarios.

Minimax Classification with 0-1 Loss and Performance Guarantees

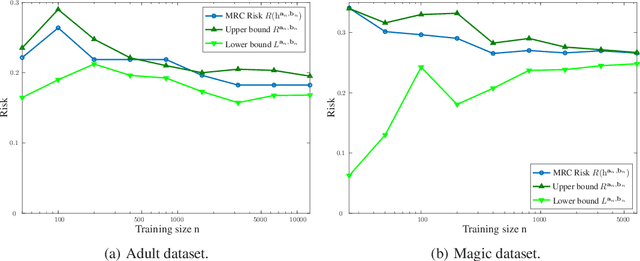
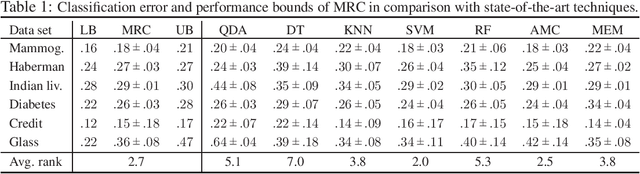
Supervised classification techniques use training samples to find classification rules with small expected 0-1 loss. Conventional methods achieve efficient learning and out-of-sample generalization by minimizing surrogate losses over specific families of rules. This paper presents minimax risk classifiers (MRCs) that do not rely on a choice of surrogate loss and family of rules. MRCs achieve efficient learning and out-of-sample generalization by minimizing worst-case expected 0-1 loss w.r.t. uncertainty sets that are defined by linear constraints and include the true underlying distribution. In addition, MRCs' learning stage provides performance guarantees as lower and upper tight bounds for expected 0-1 loss. We also present MRCs' finite-sample generalization bounds in terms of training size and smallest minimax risk, and show their competitive classification performance w.r.t. state-of-the-art techniques using benchmark datasets.

Generalized Maximum Entropy for Supervised Classification

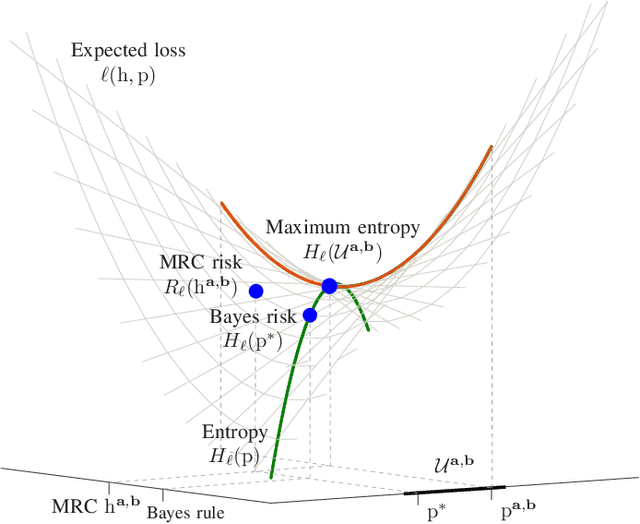
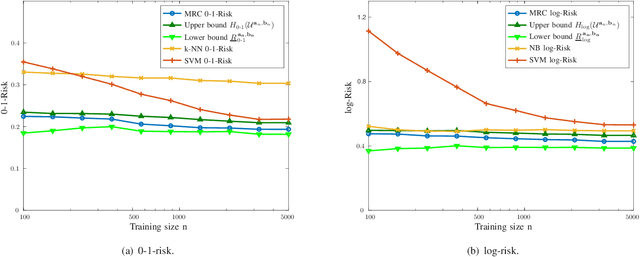
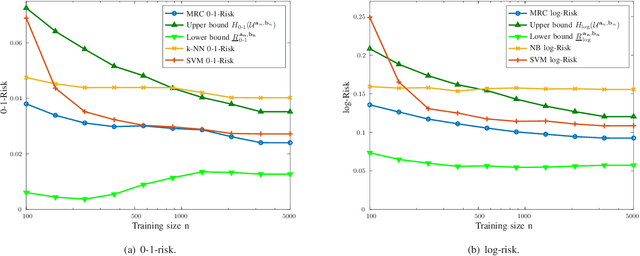
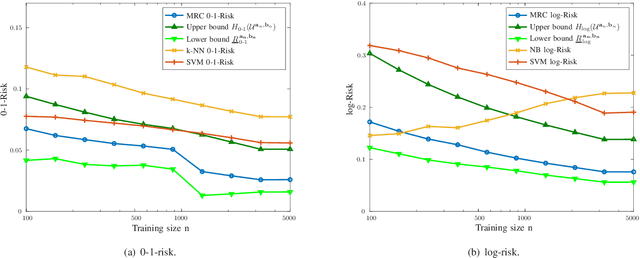
The maximum entropy principle advocates to evaluate events' probabilities using a distribution that maximizes entropy among those that satisfy certain expectations' constraints. Such principle can be generalized for arbitrary decision problems where it corresponds to minimax approaches. This paper establishes a framework for supervised classification based on the generalized maximum entropy principle that leads to minimax risk classifiers (MRCs). We develop learning techniques that determine MRCs for general entropy functions and provide performance guarantees by means of convex optimization. In addition, we describe the relationship of the presented techniques with existing classification methods, and quantify MRCs performance in comparison with the proposed bounds and conventional methods.

Supervised classification via minimax probabilistic transformations

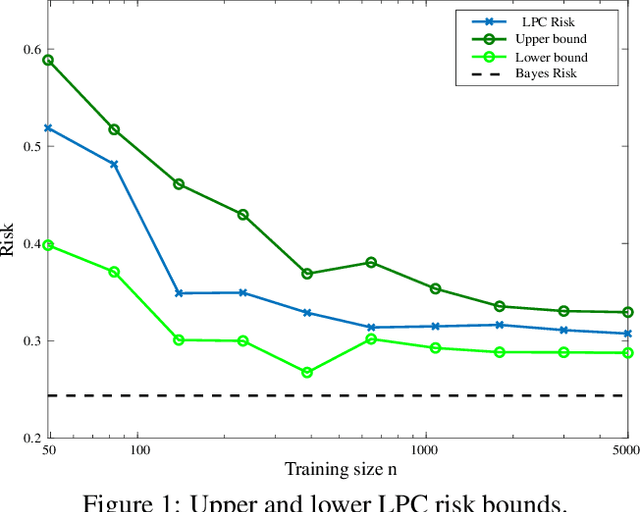
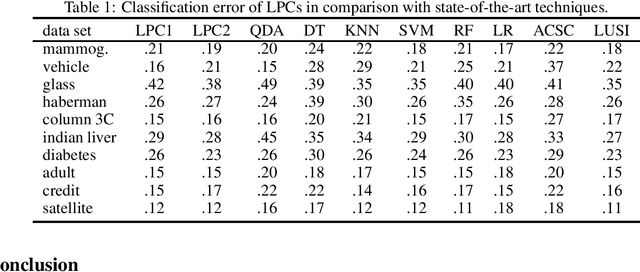
Current leaning techniques for supervised classification consider classification rules in specific families and empirically quantify performance using test data. Selection among families of classification rules, techniques' choices, parameters, etc. is mostly guided by an experimentation stage in which the performance of different options is estimated by computing the corresponding empirical risks over a set of test examples. This empirically-based system design is inefficient and not robust since it requires to test a possibly large pool of choices and it relies in the reliability of the empirical performance quantification. This paper presents classification algorithms that we call linear probabilistic machines (LPMs) that consider unconstrained classification rules and obtain tight performance guaranties during learning. LPMs utilize polyhedral uncertainty sets that contain the actual probability distribution with a tunable confidence and are defined by a functional that assigns features-label pairs to real numbers. LPMs achieve smaller worst-case risk against such uncertainty sets than any classification rule and their performance can be efficiently upper and lower bounded without testing.

General Supervision via Probabilistic Transformations

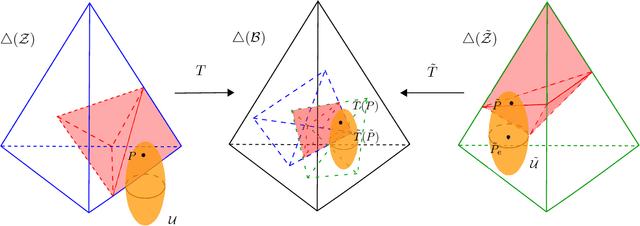
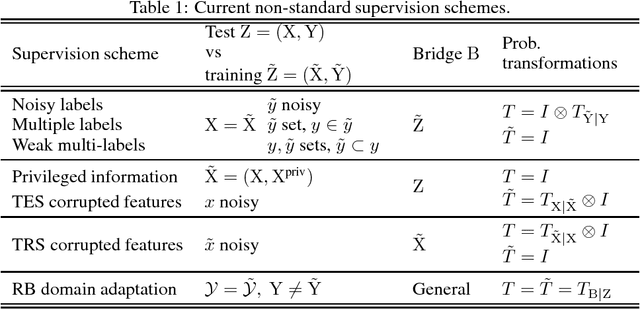
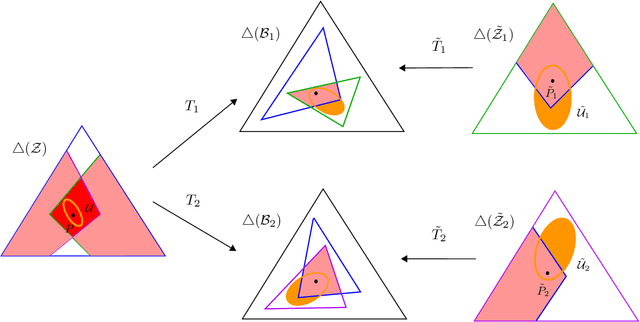
Different types of training data have led to numerous schemes for supervised classification. Current learning techniques are tailored to one specific scheme and cannot handle general ensembles of training data. This paper presents a unifying framework for supervised classification with general ensembles of training data, and proposes the learning methodology of generalized robust risk minimization (GRRM). The paper shows how current and novel supervision schemes can be addressed under the proposed framework by representing the relationship between examples at test and training via probabilistic transformations. The results show that GRRM can handle different types of training data in a unified manner, and enable new supervision schemes that aggregate general ensembles of training data.