Batched Nonparametric Bandits via k-Nearest Neighbor UCB

We study sequential decision-making in batched nonparametric contextual bandits, where actions are selected over a finite horizon divided into a small number of batches. Motivated by constraints in domains such as medicine and marketing -- where online feedback is limited -- we propose a nonparametric algorithm that combines adaptive k-nearest neighbor (k-NN) regression with the upper confidence bound (UCB) principle. Our method, BaNk-UCB, is fully nonparametric, adapts to the context dimension, and is simple to implement. Unlike prior work relying on parametric or binning-based estimators, BaNk-UCB uses local geometry to estimate rewards and adaptively balances exploration and exploitation. We provide near-optimal regret guarantees under standard Lipschitz smoothness and margin assumptions, using a theoretically motivated batch schedule that balances regret across batches and achieves minimax-optimal rates. Empirical evaluations on synthetic and real-world datasets demonstrate that BaNk-UCB consistently outperforms binning-based baselines.

Kernel $ε$-Greedy for Contextual Bandits

We consider a kernelized version of the $\epsilon$-greedy strategy for contextual bandits. More precisely, in a setting with finitely many arms, we consider that the mean reward functions lie in a reproducing kernel Hilbert space (RKHS). We propose an online weighted kernel ridge regression estimator for the reward functions. Under some conditions on the exploration probability sequence, $\{\epsilon_t\}_t$, and choice of the regularization parameter, $\{\lambda_t\}_t$, we show that the proposed estimator is consistent. We also show that for any choice of kernel and the corresponding RKHS, we achieve a sub-linear regret rate depending on the intrinsic dimensionality of the RKHS. Furthermore, we achieve the optimal regret rate of $\sqrt{T}$ under a margin condition for finite-dimensional RKHS.

Adaptive estimation of a function from its Exponential Radon Transform in presence of noise

In this article we propose a locally adaptive strategy for estimating a function from its Exponential Radon Transform (ERT) data, without prior knowledge of the smoothness of functions that are to be estimated. We build a non-parametric kernel type estimator and show that for a class of functions comprising a wide Sobolev regularity scale, our proposed strategy follows the minimax optimal rate up to a $\log{n}$ factor. We also show that there does not exist an optimal adaptive estimator on the Sobolev scale when the pointwise risk is used and in fact the rate achieved by the proposed estimator is the adaptive rate of convergence.

To update or not to update? Delayed Nonparametric Bandits with Randomized Allocation

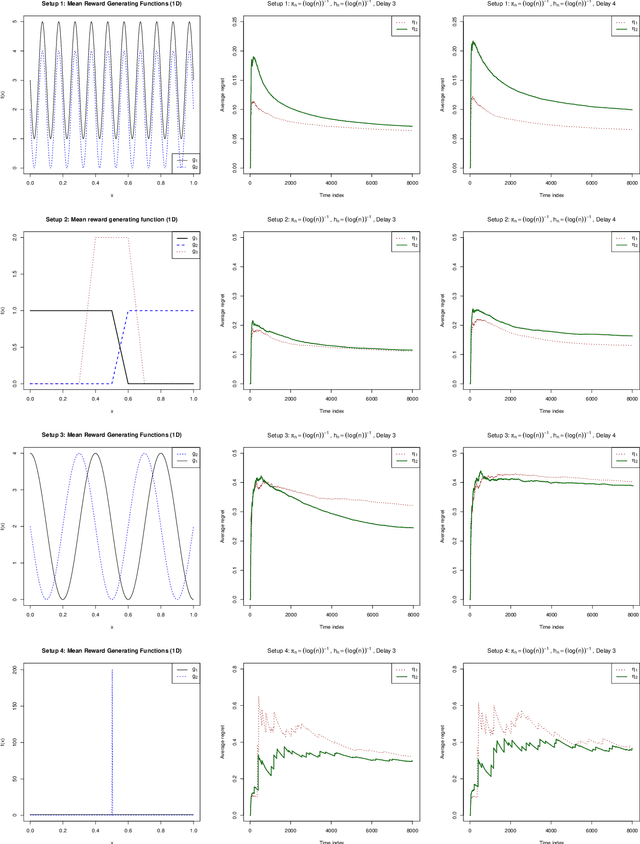
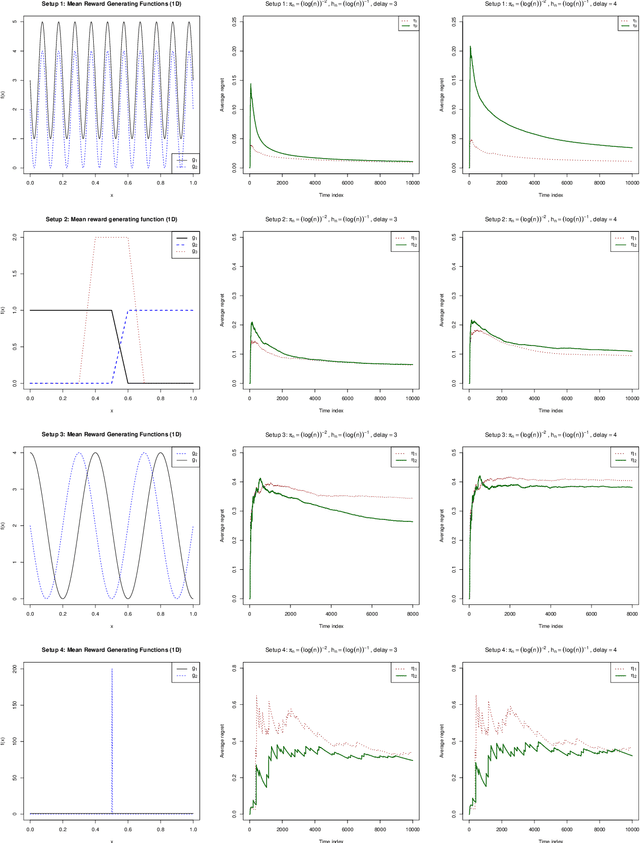
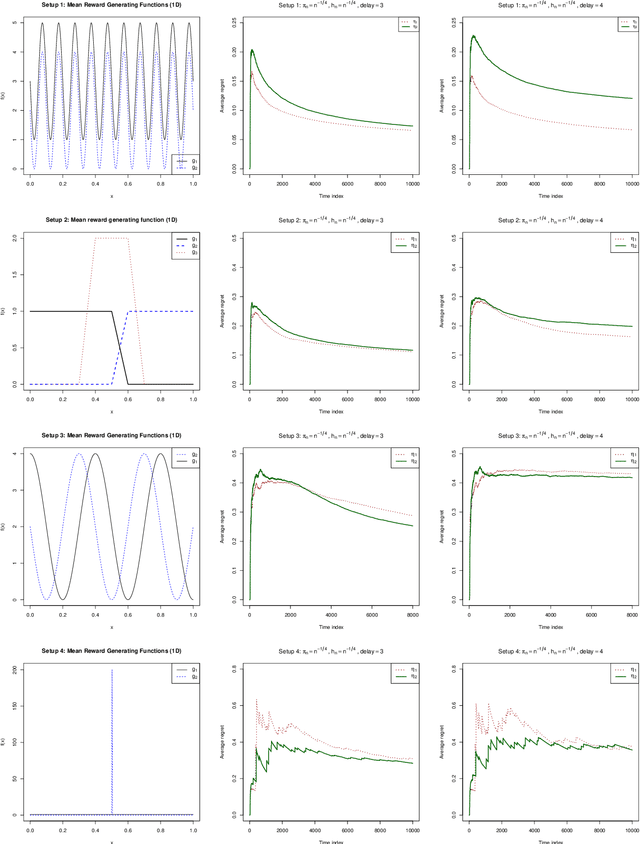
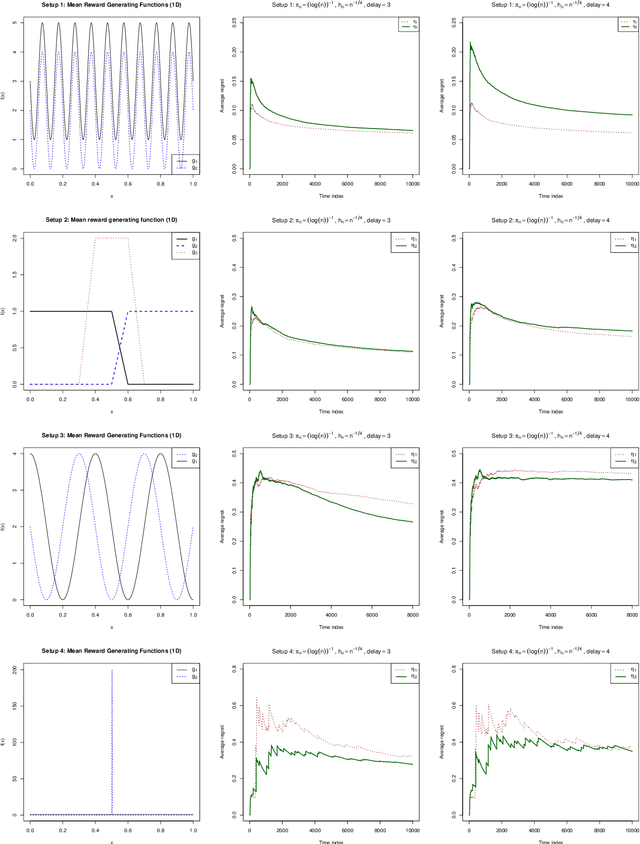
Delayed rewards problem in contextual bandits has been of interest in various practical settings. We study randomized allocation strategies and provide an understanding on how the exploration-exploitation tradeoff is affected by delays in observing the rewards. In randomized strategies, the extent of exploration-exploitation is controlled by a user-determined exploration probability sequence. In the presence of delayed rewards, one may choose between using the original exploration sequence that updates at every time point or update the sequence only when a new reward is observed, leading to two competing strategies. In this work, we show that while both strategies may lead to strong consistency in allocation, the property holds for a wider scope of situations for the latter. However, for finite sample performance, we illustrate that both strategies have their own advantages and disadvantages, depending on the severity of the delay and underlying reward generating mechanisms.

Randomized Allocation with Nonparametric Estimation for Contextual Multi-Armed Bandits with Delayed Rewards

We study a multi-armed bandit problem with covariates in a setting where there is a possible delay in observing the rewards. Under some mild assumptions on the probability distributions for the delays and using an appropriate randomization to select the arms, the proposed strategy is shown to be strongly consistent.