Limits of message passing for node classification: How class-bottlenecks restrict signal-to-noise ratio

Message passing neural networks (MPNNs) are powerful models for node classification but suffer from performance limitations under heterophily (low same-class connectivity) and structural bottlenecks in the graph. We provide a unifying statistical framework exposing the relationship between heterophily and bottlenecks through the signal-to-noise ratio (SNR) of MPNN representations. The SNR decomposes model performance into feature-dependent parameters and feature-independent sensitivities. We prove that the sensitivity to class-wise signals is bounded by higher-order homophily -- a generalisation of classical homophily to multi-hop neighbourhoods -- and show that low higher-order homophily manifests locally as the interaction between structural bottlenecks and class labels (class-bottlenecks). Through analysis of graph ensembles, we provide a further quantitative decomposition of bottlenecking into underreaching (lack of depth implying signals cannot arrive) and oversquashing (lack of breadth implying signals arriving on fewer paths) with closed-form expressions. We prove that optimal graph structures for maximising higher-order homophily are disjoint unions of single-class and two-class-bipartite clusters. This yields BRIDGE, a graph ensemble-based rewiring algorithm that achieves near-perfect classification accuracy across all homophily regimes on synthetic benchmarks and significant improvements on real-world benchmarks, by eliminating the ``mid-homophily pitfall'' where MPNNs typically struggle, surpassing current standard rewiring techniques from the literature. Our framework, whose code we make available for public use, provides both diagnostic tools for assessing MPNN performance, and simple yet effective methods for enhancing performance through principled graph modification.

Geodesic statistics for random network families

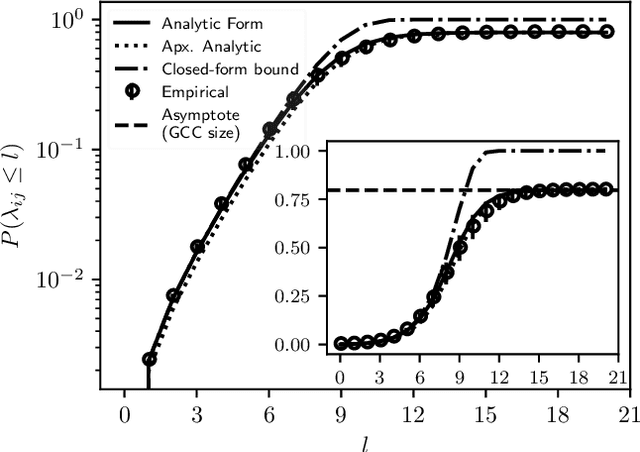
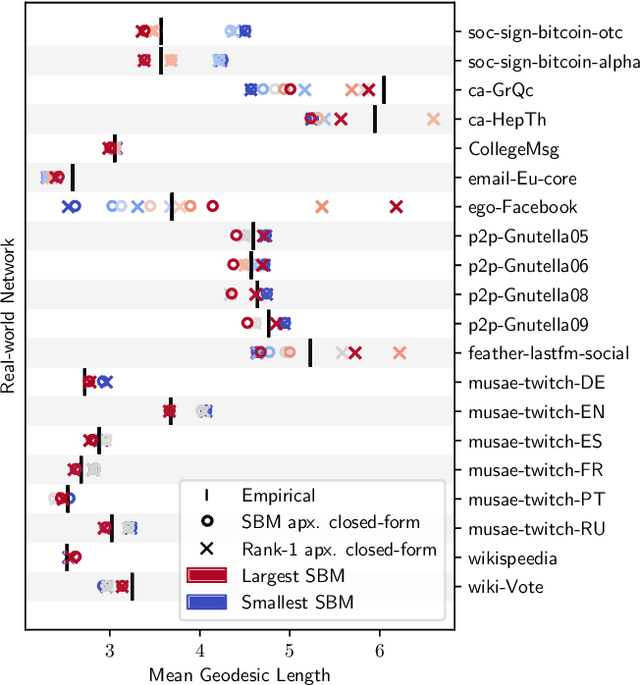
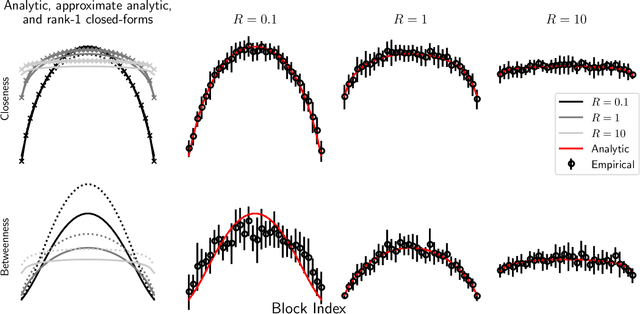
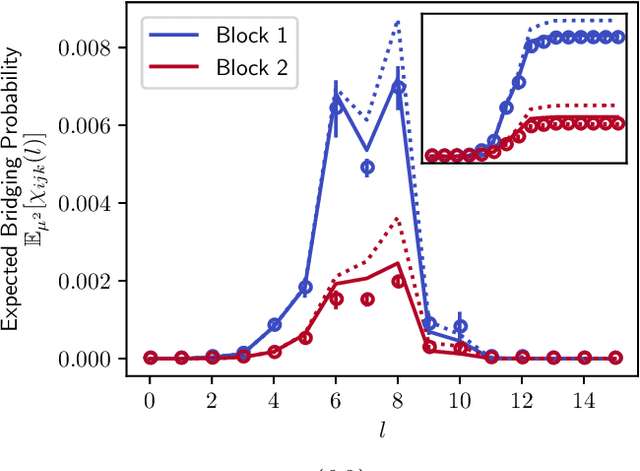
A key task in the study of networked systems is to derive local and global properties that impact connectivity, synchronizability, and robustness. Computing shortest paths or geodesics in the network yields measures of node centrality and network connectivity that can contribute to explain such phenomena. We derive an analytic distribution of shortest path lengths, on the giant component in the supercritical regime or on small components in the subcritical regime, of any sparse (possibly directed) graph with conditionally independent edges, in the infinite-size limit. We provide specific results for widely used network families like stochastic block models, dot-product graphs, random geometric graphs, and graphons. The survival function of the shortest path length distribution possesses a simple closed-form lower bound which is asymptotically tight for finite lengths, has a natural interpretation of traversing independent geodesics in the network, and delivers novel insight in the above network families. Notably, the shortest path length distribution allows us to derive, for the network families above, important graph properties like the bond percolation threshold, size of the giant component, average shortest path length, and closeness and betweenness centralities. We also provide a corroborative analysis of a set of 20 empirical networks. This unifying framework demonstrates how geodesic statistics for a rich family of random graphs can be computed cheaply without having access to true or simulated networks, especially when they are sparse but prohibitively large.