Improved Complexities for Stochastic Conditional Gradient Methods under Interpolation-like Conditions

We analyze stochastic conditional gradient type methods for constrained optimization problems arising in over-parametrized machine learning. We show that one could leverage the interpolation-like conditions satisfied by such models to obtain improved complexities for conditional gradient type methods. For the aforementioned class of problem, when the objective function is convex, we show that the conditional gradient method requires $\mathcal{O}(\epsilon^{-2})$ calls to the stochastic gradient oracle to find an $\epsilon$-optimal solution. Furthermore, by including a gradient sliding step, the number of calls reduces to $\mathcal{O}(\epsilon^{-1.5})$. We also establish similar improved results in the zeroth-order setting, where only noisy function evaluations are available. Notably, the above results are achieved without any variance reduction techniques, thereby demonstrating the improved performance of vanilla versions of conditional gradient methods for over-parametrized machine learning problems.

Multi-Point Bandit Algorithms for Nonstationary Online Nonconvex Optimization

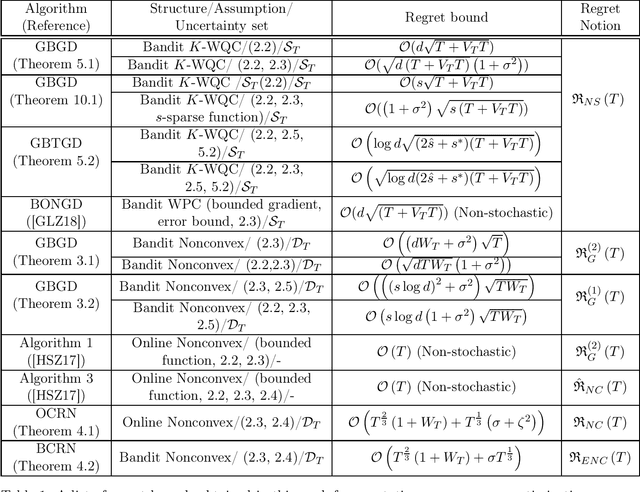
Bandit algorithms have been predominantly analyzed in the convex setting with function-value based stationary regret as the performance measure. In this paper, motivated by online reinforcement learning problems, we propose and analyze bandit algorithms for both general and structured nonconvex problems with nonstationary (or dynamic) regret as the performance measure, in both stochastic and non-stochastic settings. First, for general nonconvex functions, we consider nonstationary versions of first-order and second-order stationary solutions as a regret measure, motivated by similar performance measures for offline nonconvex optimization. In the case of second-order stationary solution based regret, we propose and analyze online and bandit versions of the cubic regularized Newton's method. The bandit version is based on estimating the Hessian matrices in the bandit setting, based on second-order Gaussian Stein's identity. Our nonstationary regret bounds in terms of second-order stationary solutions have interesting consequences for avoiding saddle points in the bandit setting. Next, for weakly quasi convex functions and monotone weakly submodular functions we consider nonstationary regret measures in terms of function-values; such structured classes of nonconvex functions enable one to consider regret measure defined in terms of function values, similar to convex functions. For this case of function-value, and first-order stationary solution based regret measures, we provide regret bounds in both the low- and high-dimensional settings, for some scenarios.

Non-asymptotic Results for Langevin Monte Carlo: Coordinate-wise and Black-box Sampling

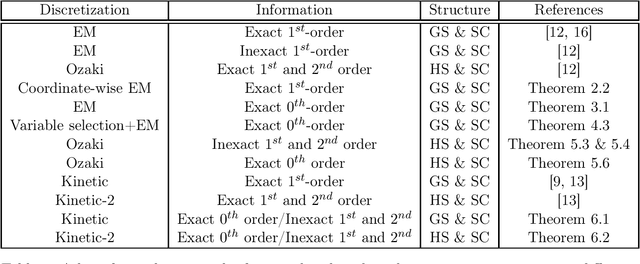
Discretization of continuous-time diffusion processes, using gradient and Hessian information, is a popular technique for sampling. For example, the Euler-Maruyama discretization of the Langevin diffusion process, called as Langevin Monte Carlo (LMC), is a canonical algorithm for sampling from strongly log-concave densities. In this work, we make several theoretical contributions to the literature on such sampling techniques. Specifically, we first provide a Randomized Coordinate-wise LMC algorithm suitable for large-scale sampling problems and provide a theoretical analysis. We next consider the case of zeroth-order or black-box sampling where one only obtains evaluates of the density. Based on Gaussian Stein's identities we then estimate the gradient and Hessian information and leverage it in the context of black-box sampling. We then provide a theoretical analysis of gradient and Hessian based discretizations of Langevin and kinetic Langevin diffusion processes for sampling, quantifying the non-asymptotic accuracy. We also consider high-dimensional black-box sampling under the assumption that the density depends only on a small subset of the entire coordinates. We propose a variable selection technique based on zeroth-order gradient estimates and establish its theoretical guarantees. Our theoretical contributions extend the practical applicability of sampling algorithms to the large-scale, black-box and high-dimensional settings.

Zeroth-order (Non)-Convex Stochastic Optimization via Conditional Gradient and Gradient Updates

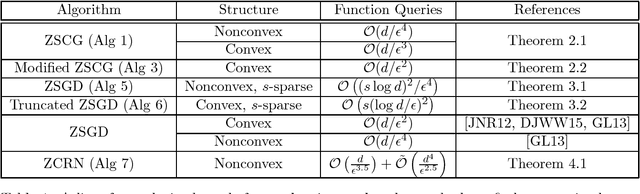
In this paper, we propose and analyze zeroth-order stochastic approximation algorithms for nonconvex and convex optimization. Specifically, we propose generalizations of the conditional gradient algorithm achieving rates similar to the standard stochastic gradient algorithm using only zeroth-order information. Furthermore, under a structural sparsity assumption, we first illustrate an implicit regularization phenomenon where the standard stochastic gradient algorithm with zeroth-order information adapts to the sparsity of the problem at hand by just varying the step-size. Next, we propose a truncated stochastic gradient algorithm with zeroth-order information, whose rate depends only poly-logarithmically on the dimensionality.

Generalized Uniformly Optimal Methods for Nonlinear Programming

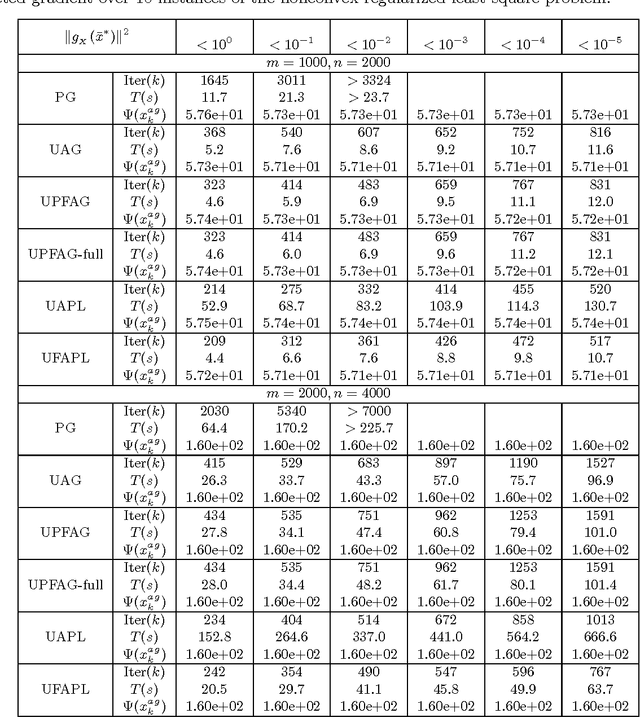
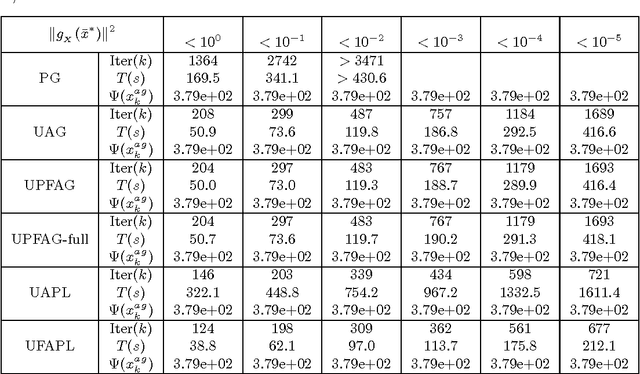
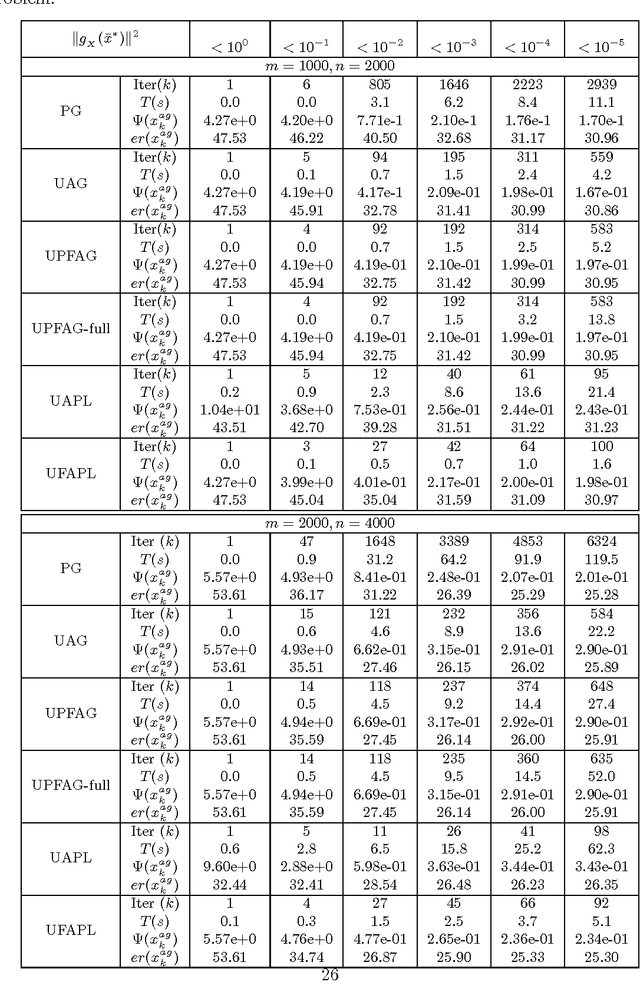
In this paper, we present a generic framework to extend existing uniformly optimal convex programming algorithms to solve more general nonlinear, possibly nonconvex, optimization problems. The basic idea is to incorporate a local search step (gradient descent or Quasi-Newton iteration) into these uniformly optimal convex programming methods, and then enforce a monotone decreasing property of the function values computed along the trajectory. Algorithms of these types will then achieve the best known complexity for nonconvex problems, and the optimal complexity for convex ones without requiring any problem parameters. As a consequence, we can have a unified treatment for a general class of nonlinear programming problems regardless of their convexity and smoothness level. In particular, we show that the accelerated gradient and level methods, both originally designed for solving convex optimization problems only, can be used for solving both convex and nonconvex problems uniformly. In a similar vein, we show that some well-studied techniques for nonlinear programming, e.g., Quasi-Newton iteration, can be embedded into optimal convex optimization algorithms to possibly further enhance their numerical performance. Our theoretical and algorithmic developments are complemented by some promising numerical results obtained for solving a few important nonconvex and nonlinear data analysis problems in the literature.

Stochastic First- and Zeroth-order Methods for Nonconvex Stochastic Programming

In this paper, we introduce a new stochastic approximation (SA) type algorithm, namely the randomized stochastic gradient (RSG) method, for solving an important class of nonlinear (possibly nonconvex) stochastic programming (SP) problems. We establish the complexity of this method for computing an approximate stationary point of a nonlinear programming problem. We also show that this method possesses a nearly optimal rate of convergence if the problem is convex. We discuss a variant of the algorithm which consists of applying a post-optimization phase to evaluate a short list of solutions generated by several independent runs of the RSG method, and show that such modification allows to improve significantly the large-deviation properties of the algorithm. These methods are then specialized for solving a class of simulation-based optimization problems in which only stochastic zeroth-order information is available.