VocSim: A Training-free Benchmark for Zero-shot Content Identity in Single-source Audio

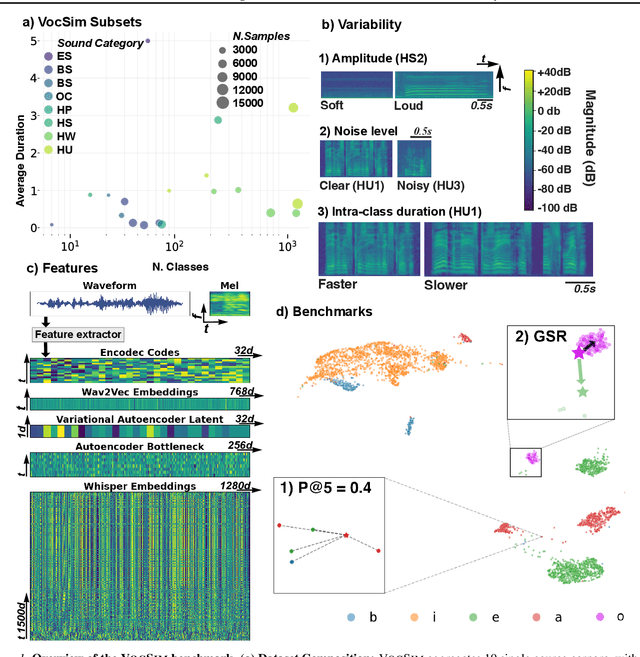
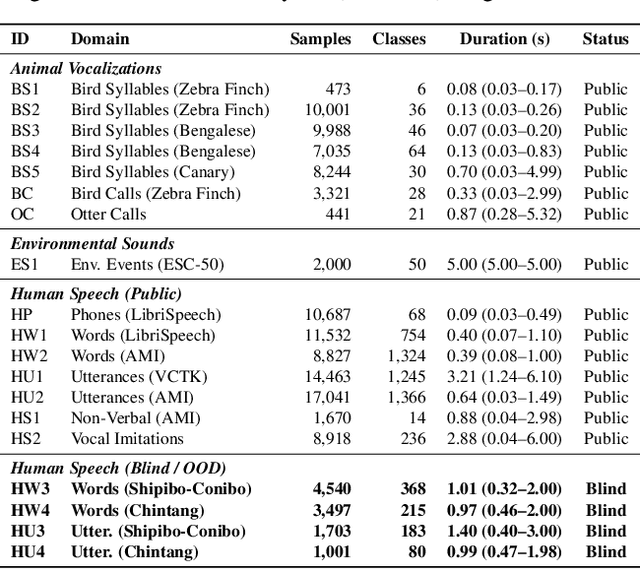
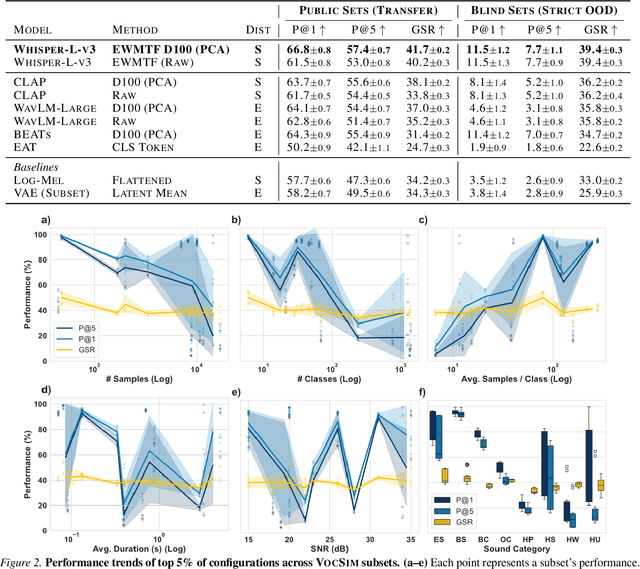
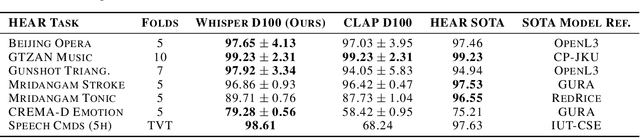
General-purpose audio representations aim to map acoustically variable instances of the same event to nearby points, resolving content identity in a zero-shot setting. Unlike supervised classification benchmarks that measure adaptability via parameter updates, we introduce VocSim, a training-free benchmark probing the intrinsic geometric alignment of frozen embeddings. VocSim aggregates 125k single-source clips from 19 corpora spanning human speech, animal vocalizations, and environmental sounds. By restricting to single-source audio, we isolate content representation from the confound of source separation. We evaluate embeddings using Precision@k for local purity and the Global Separation Rate (GSR) for point-wise class separation. To calibrate GSR, we report lift over an empirical permutation baseline. Across diverse foundation models, a simple pipeline, frozen Whisper encoder features, time-frequency pooling, and label-free PCA, yields strong zero-shot performance. However, VocSim also uncovers a consistent generalization gap. On blind, low-resource speech, local retrieval drops sharply. While performance remains statistically distinguishable from chance, the absolute geometric structure collapses, indicating a failure to generalize to unseen phonotactics. As external validation, our top embeddings predict avian perceptual similarity, improve bioacoustic classification, and achieve state-of-the-art results on the HEAR benchmark. We posit that the intrinsic geometric quality measured here proxies utility in unlisted downstream applications. We release data, code, and a public leaderboard to standardize the evaluation of intrinsic audio geometry.

Time-series Random Process Complexity Ranking Using a Bound on Conditional Differential Entropy

Conditional differential entropy provides an intuitive measure for relatively ranking time-series complexity by quantifying uncertainty in future observations given past context. However, its direct computation for high-dimensional processes from unknown distributions is often intractable. This paper builds on the information theoretic prediction error bounds established by Fang et al. \cite{fang2019generic}, which demonstrate that the conditional differential entropy \textbf{$h(X_k \mid X_{k-1},...,X_{k-m})$} is upper bounded by a function of the determinant of the covariance matrix of next-step prediction errors for any next step prediction model. We add to this theoretical framework by further increasing this bound by leveraging Hadamard's inequality and the positive semi-definite property of covariance matrices. To see if these bounds can be used to rank the complexity of time series, we conducted two synthetic experiments: (1) controlled linear autoregressive processes with additive Gaussian noise, where we compare ordinary least squares prediction error entropy proxies to the true entropies of various additive noises, and (2) a complexity ranking task of bio-inspired synthetic audio data with unknown entropy, where neural network prediction errors are used to recover the known complexity ordering. This framework provides a computationally tractable method for time-series complexity ranking using prediction errors from next-step prediction models, that maintains a theoretical foundation in information theory.