Quantum Natural Stochastic Pairwise Coordinate Descent

Quantum machine learning through variational quantum algorithms (VQAs) has gained substantial attention in recent years. VQAs employ parameterized quantum circuits, which are typically optimized using gradient-based methods. However, these methods often exhibit sub-optimal convergence performance due to their dependence on Euclidean geometry. The quantum natural gradient descent (QNGD) optimization method, which considers the geometry of the quantum state space via a quantum information (Riemannian) metric tensor, provides a more effective optimization strategy. Despite its advantages, QNGD encounters notable challenges for learning from quantum data, including the no-cloning principle, which prohibits the replication of quantum data, state collapse, and the measurement postulate, which leads to the stochastic loss function. This paper introduces the quantum natural stochastic pairwise coordinate descent (2-QNSCD) optimization method. This method leverages the curved geometry of the quantum state space through a novel ensemble-based quantum information metric tensor, offering a more physically realizable optimization strategy for learning from quantum data. To improve computational efficiency and reduce sample complexity, we develop a highly sparse unbiased estimator of the novel metric tensor using a quantum circuit with gate complexity $\Theta(1)$ times that of the parameterized quantum circuit and single-shot quantum measurements. Our approach avoids the need for multiple copies of quantum data, thus adhering to the no-cloning principle. We provide a detailed theoretical foundation for our optimization method, along with an exponential convergence analysis. Additionally, we validate the utility of our method through a series of numerical experiments.

Capacity-achieving Polar-based Codes with Sparsity Constraints on the Generator Matrices

In this paper, we leverage polar codes and the well-established channel polarization to design capacity-achieving codes with a certain constraint on the weights of all the columns in the generator matrix (GM) while having a low-complexity decoding algorithm. We first show that given a binary-input memoryless symmetric (BMS) channel $W$ and a constant $s \in (0, 1]$, there exists a polarization kernel such that the corresponding polar code is capacity-achieving with the \textit{rate of polarization} $s/2$, and the GM column weights being bounded from above by $N^s$. To improve the sparsity versus error rate trade-off, we devise a column-splitting algorithm and two coding schemes for BEC and then for general BMS channels. The \textit{polar-based} codes generated by the two schemes inherit several fundamental properties of polar codes with the original $2 \times 2$ kernel including the decay in error probability, decoding complexity, and the capacity-achieving property. Furthermore, they demonstrate the additional property that their GM column weights are bounded from above sublinearly in $N$, while the original polar codes have some column weights that are linear in $N$. In particular, for any BEC and $\beta <0.5$, the existence of a sequence of capacity-achieving polar-based codes where all the GM column weights are bounded from above by $N^\lambda$ with $\lambda \approx 0.585$, and with the error probability bounded by $O(2^{-N^{\beta}} )$ under a decoder with complexity $O(N\log N)$, is shown. The existence of similar capacity-achieving polar-based codes with the same decoding complexity is shown for any BMS channel and $\beta <0.5$ with $\lambda \approx 0.631$.

Lattices from Linear Codes: Source and Channel Networks

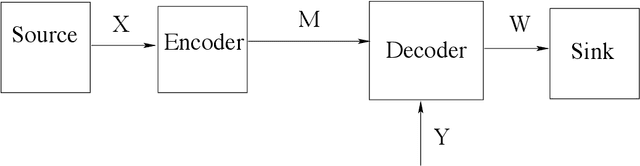
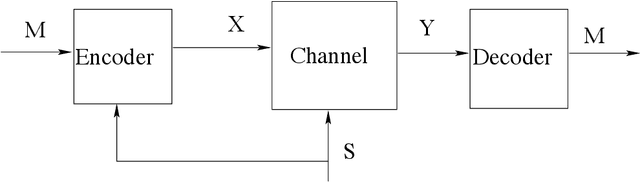
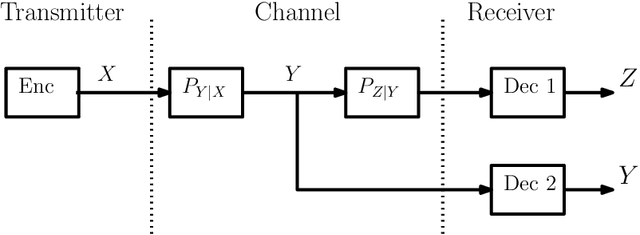
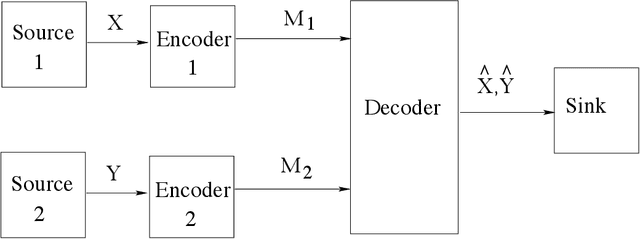
In this paper, we consider the information-theoretic characterization of the set of achievable rates and distortions in a broad class of multiterminal communication scenarios with general continuous-valued sources and channels. A framework is presented which involves fine discretization of the source and channel variables followed by communication over the resulting discretized network. In order to evaluate fundamental performance limits, convergence results for information measures are provided under the proposed discretization process. Using this framework, we consider point-to-point source coding and channel coding with side-information, distributed source coding with distortion constraints, the function reconstruction problems (two-help-one), computation over multiple access channel, the interference channel, and the multiple-descriptions source coding problem. We construct lattice-like codes for general sources and channels, and derive inner-bounds to set of achievable rates and distortions in these communication scenarios.

New Bounds on the Size of Binary Codes with Large Minimum Distance

Let A(n, d) denote the maximum number of codewords in a binary code of length n and minimum Hamming distance d. Deriving upper and lower bounds on A(n, d) have been a subject for extensive research in coding theory. In this paper, we examine upper and lower bounds on A(n, d) in the high-minimum distance regime, in particular, when $d = n/2 - \Theta(\sqrt{n})$. We will first provide a lower bound based on a cyclic construction for codes of length $n= 2^m -1$ and show that $A(n, d= n/2 - 2^{c-1}\sqrt{n}) \geq n^c$, where c is an integer with $1 \leq c \leq m/2-1$. With a Fourier-analytic view of Delsarte's linear program, novel upper bounds on $A(n, n/2 - \sqrt{n})$ and $A(n, n/2 - 2 \sqrt{n})$ are obtained, and, to the best of the authors' knowledge, are the first upper bounds scaling polynomially in n for the regime with $d = n/2 - \Theta(\sqrt{n})$.

Coding for Crowdsourced Classification with XOR Queries

This paper models the crowdsourced labeling/classification problem as a sparsely encoded source coding problem, where each query answer, regarded as a code bit, is the XOR of a small number of labels, as source information bits. In this paper we leverage the connections between this problem and well-studied codes with sparse representations for the channel coding problem to provide querying schemes with almost optimal number of queries, each of which involving only a constant number of labels. We also extend this scenario to the case where some workers can be unresponsive. For this case, we propose querying schemes where each query involves only log n items, where n is the total number of items to be labeled. Furthermore, we consider classification of two correlated labeling systems and provide two-stage querying schemes with almost optimal number of queries each involving a constant number of labels.