Accelerating Part-Scale Simulation in Liquid Metal Jet Additive Manufacturing via Operator Learning

Predicting part quality for additive manufacturing (AM) processes requires high-fidelity numerical simulation of partial differential equations (PDEs) governing process multiphysics on a scale of minimum manufacturable features. This makes part-scale predictions computationally demanding, especially when they require many small-scale simulations. We consider drop-on-demand liquid metal jetting (LMJ) as an illustrative example of such computational complexity. A model describing droplet coalescence for LMJ may include coupled incompressible fluid flow, heat transfer, and phase change equations. Numerically solving these equations becomes prohibitively expensive when simulating the build process for a full part consisting of thousands to millions of droplets. Reduced-order models (ROMs) based on neural networks (NN) or k-nearest neighbor (kNN) algorithms have been built to replace the original physics-based solver and are computationally tractable for part-level simulations. However, their quick inference capabilities often come at the expense of accuracy, robustness, and generalizability. We apply an operator learning (OL) approach to learn a mapping between initial and final states of the droplet coalescence process for enabling rapid and accurate part-scale build simulation. Preliminary results suggest that OL requires order-of-magnitude fewer data points than a kNN approach and is generalizable beyond the training set while achieving similar prediction error.

Mutual Information for Explainable Deep Learning of Multiscale Systems

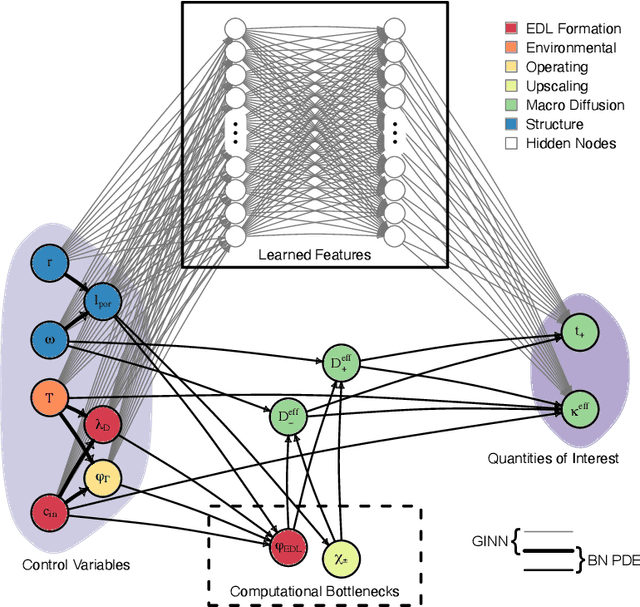
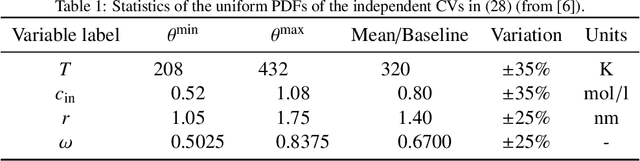
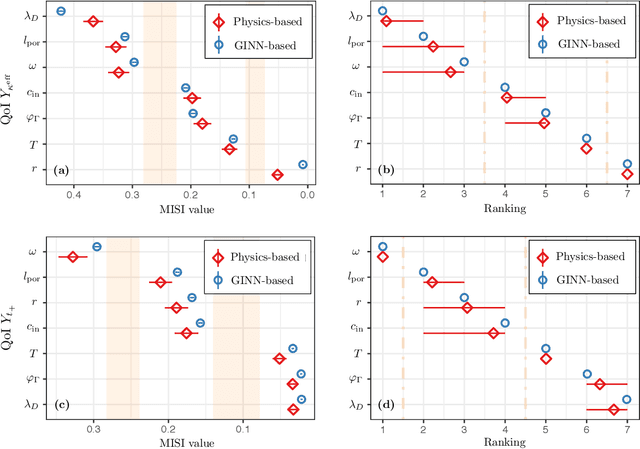
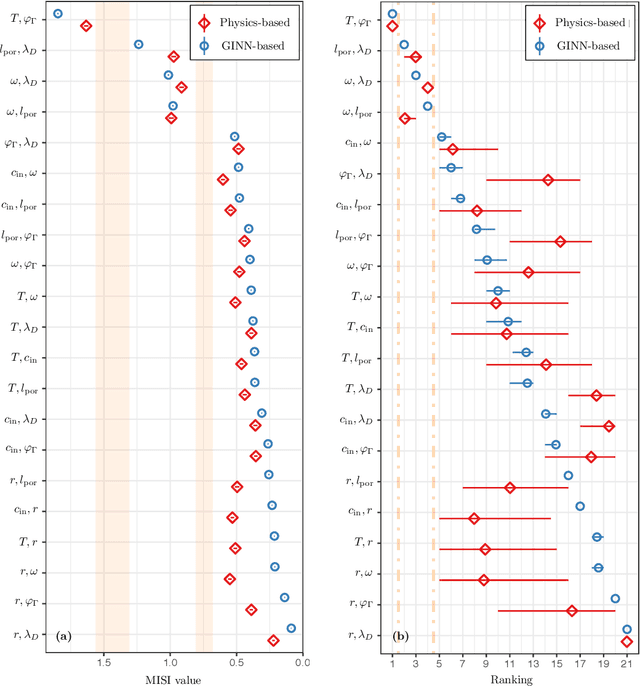
Timely completion of design cycles for multiscale and multiphysics systems ranging from consumer electronics to hypersonic vehicles relies on rapid simulation-based prototyping. The latter typically involves high-dimensional spaces of possibly correlated control variables (CVs) and quantities of interest (QoIs) with non-Gaussian and/or multimodal distributions. We develop a model-agnostic, moment-independent global sensitivity analysis (GSA) that relies on differential mutual information to rank the effects of CVs on QoIs. Large amounts of data, which are necessary to rank CVs with confidence, are cheaply generated by a deep neural network (DNN) surrogate model of the underlying process. The DNN predictions are made explainable by the GSA so that the DNN can be deployed to close design loops. Our information-theoretic framework is compatible with a wide variety of black-box models. Its application to multiscale supercapacitor design demonstrates that the CV rankings facilitated by a domain-aware Graph-Informed Neural Network are better resolved than their counterparts obtained with a physics-based model for a fixed computational budget. Consequently, our information-theoretic GSA provides an "outer loop" for accelerated product design by identifying the most and least sensitive input directions and performing subsequent optimization over appropriately reduced parameter subspaces.

GINNs: Graph-Informed Neural Networks for Multiscale Physics

We introduce the concept of a Graph-Informed Neural Network (GINN), a hybrid approach combining deep learning with probabilistic graphical models (PGMs) that acts as a surrogate for physics-based representations of multiscale and multiphysics systems. GINNs address the twin challenges of removing intrinsic computational bottlenecks in physics-based models and generating large data sets for estimating probability distributions of quantities of interest (QoIs) with a high degree of confidence. Both the selection of the complex physics learned by the NN and its supervised learning/prediction are informed by the PGM, which includes the formulation of structured priors for tunable control variables (CVs) to account for their mutual correlations and ensure physically sound CV and QoI distributions. GINNs accelerate the prediction of QoIs essential for simulation-based decision-making where generating sufficient sample data using physics-based models alone is often prohibitively expensive. Using a real-world application grounded in supercapacitor-based energy storage, we describe the construction of GINNs from a Bayesian network-embedded homogenized model for supercapacitor dynamics, and demonstrate their ability to produce kernel density estimates of relevant non-Gaussian, skewed QoIs with tight confidence intervals.