Atmospheric Density-Compensating Model Predictive Control for Targeted Reentry of Drag-Modulated Spacecraft

This paper presents an estimation and control framework that enables the targeted reentry of a drag-modulated spacecraft in the presence of atmospheric density uncertainty. In particular, an extended Kalman filter (EKF) is used to estimate the in-flight density errors relative to the atmospheric density used to generate the nominal guidance trajectory. This information is leveraged within a model predictive control (MPC) strategy to improve tracking performance, reduce control effort, and increase robustness to actuator saturation compared to the state-of-the-art approach. The estimation and control framework is tested in a Monte Carlo simulation campaign with historical space weather data. These simulation efforts demonstrate that the proposed framework is able to stay within 100 km of the guidance trajectory at all points in time for 98.4% of cases. The remaining 1.6% of cases were pushed away from the guidance by large density errors, many due to significant solar storms and flares, that could not physically be compensated for by the drag control device. For the successful cases, the proposed framework was able to guide the spacecraft to the desired location at the entry interface altitude with a mean error of 12.1 km and 99.7% of cases below 100 km.

Adaptive Passivity-Based Pose Tracking Control of Cable-Driven Parallel Robots for Multiple Attitude Parameterizations

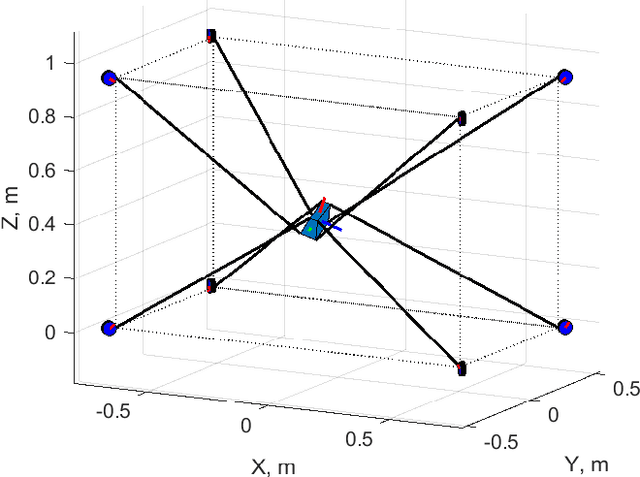
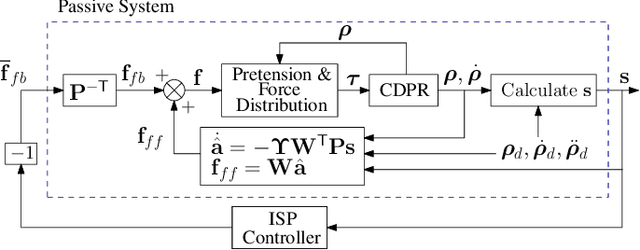
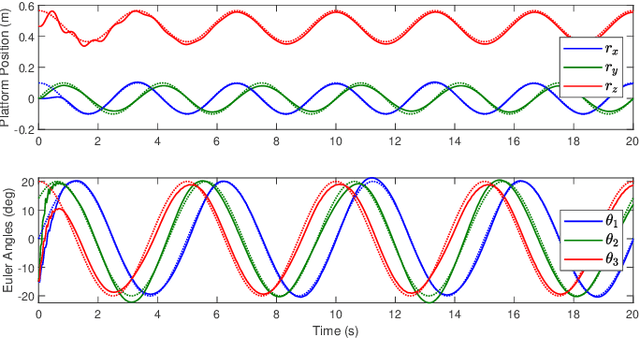
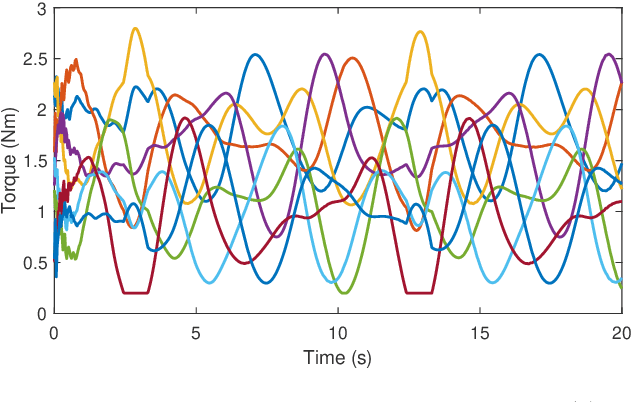
The proposed control method uses an adaptive feedforward-based controller to establish a passive input-output mapping for the CDPR that is used alongside a linear time-invariant strictly positive real feedback controller to guarantee robust closed-loop input-output stability and asymptotic pose trajectory tracking via the passivity theorem. A novelty of the proposed controller is its formulation for use with a range of payload attitude parameterizations, including any unconstrained attitude parameterization, the quaternion, or the direction cosine matrix (DCM). The performance and robustness of the proposed controller is demonstrated through numerical simulations of a CDPR with rigid and flexible cables. The results demonstrate the importance of carefully defining the CDPR's pose error, which is performed in multiplicative fashion when using the quaternion and DCM, and in a specific additive fashion when using unconstrained attitude parameters (e.g., an Euler-angle sequence).