Analysis of the Identifying Regulation with Adversarial Surrogates Algorithm

Given a time-series of noisy measured outputs of a dynamical system z[k], k=1...N, the Identifying Regulation with Adversarial Surrogates (IRAS) algorithm aims to find a non-trivial first integral of the system, namely, a scalar function g() such that g(z[i]) = g(z[j]), for all i,j. IRAS has been suggested recently and was used successfully in several learning tasks in models from biology and physics. Here, we give the first rigorous analysis of this algorithm in a specific setting. We assume that the observations admit a linear first integral and that they are contaminated by Gaussian noise. We show that in this case the IRAS iterations are closely related to the self-consistent-field (SCF) iterations for solving a generalized Rayleigh quotient minimization problem. Using this approach, we derive several sufficient conditions guaranteeing local convergence of IRAS to the correct first integral.

Enhancing Causal Estimation through Unlabeled Offline Data

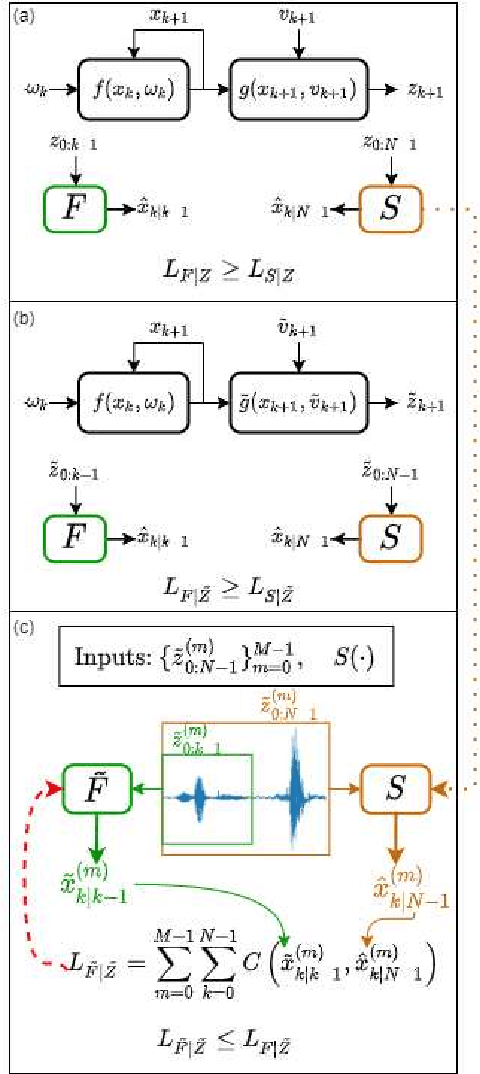
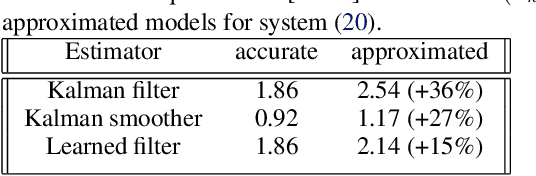
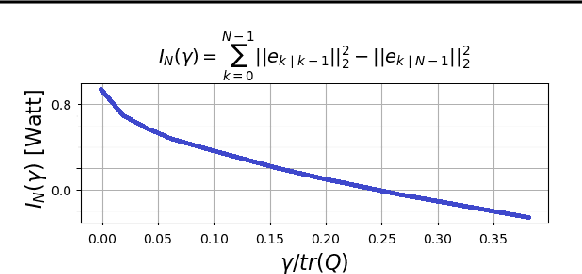
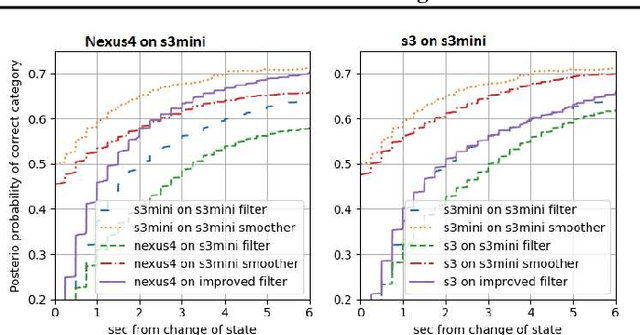
Consider a situation where a new patient arrives in the Intensive Care Unit (ICU) and is monitored by multiple sensors. We wish to assess relevant unmeasured physiological variables (e.g., cardiac contractility and output and vascular resistance) that have a strong effect on the patients diagnosis and treatment. We do not have any information about this specific patient, but, extensive offline information is available about previous patients, that may only be partially related to the present patient (a case of dataset shift). This information constitutes our prior knowledge, and is both partial and approximate. The basic question is how to best use this prior knowledge, combined with online patient data, to assist in diagnosing the current patient most effectively. Our proposed approach consists of three stages: (i) Use the abundant offline data in order to create both a non-causal and a causal estimator for the relevant unmeasured physiological variables. (ii) Based on the non-causal estimator constructed, and a set of measurements from a new group of patients, we construct a causal filter that provides higher accuracy in the prediction of the hidden physiological variables for this new set of patients. (iii) For any new patient arriving in the ICU, we use the constructed filter in order to predict relevant internal variables. Overall, this strategy allows us to make use of the abundantly available offline data in order to enhance causal estimation for newly arriving patients. We demonstrate the effectiveness of this methodology on a (non-medical) real-world task, in situations where the offline data is only partially related to the new observations. We provide a mathematical analysis of the merits of the approach in a linear setting of Kalman filtering and smoothing, demonstrating its utility.