Efficient interpolation of molecular properties across chemical compound space with low-dimensional descriptors

We demonstrate accurate data-starved models of molecular properties for interpolation in chemical compound spaces with low-dimensional descriptors. Our starting point is based on three-dimensional, universal, physical descriptors derived from the properties of the distributions of the eigenvalues of Coulomb matrices. To account for the shape and composition of molecules, we combine these descriptors with six-dimensional features informed by the Gershgorin circle theorem. We use the nine-dimensional descriptors thus obtained for Gaussian process regression based on kernels with variable functional form, leading to extremely efficient, low-dimensional interpolation models. The resulting models trained with 100 molecules are able to predict the product of entropy and temperature ($S \times T$) and zero point vibrational energy (ZPVE) with the absolute error under 1 kcal mol$^{-1}$ for $> 78$ \% and under 1.3 kcal mol$^{-1}$ for $> 92$ \% of molecules in the test data. The test data comprises 20,000 molecules with complexity varying from three atoms to 29 atoms and the ranges of $S \times T$ and ZPVE covering 36 kcal mol$^{-1}$ and 161 kcal mol$^{-1}$, respectively. We also illustrate that the descriptors based on the Gershgorin circle theorem yield more accurate models of molecular entropy than those based on graph neural networks that explicitly account for the atomic connectivity of molecules.

Universal expressiveness of variational quantum classifiers and quantum kernels for support vector machines

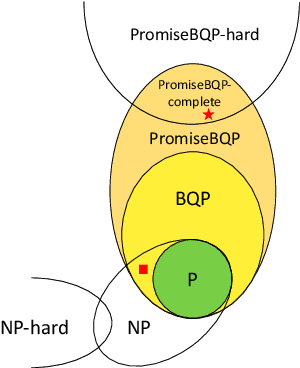
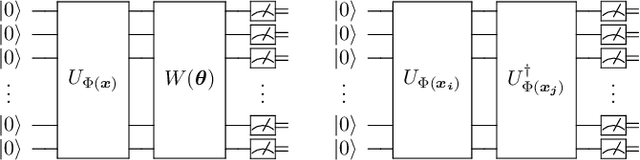
Machine learning is considered to be one of the most promising applications of quantum computing. Therefore, the search for quantum advantage of the quantum analogues of machine learning models is a key research goal. Here, we show that variational quantum classifiers (VQC) and support vector machines with quantum kernels (QSVM) can solve a classification problem based on the k-Forrelation problem, which is known to be PromiseBQP-complete. Because the PromiseBQP complexity class includes all Bounded-Error Quantum Polynomial-Time (BQP) decision problems, our results imply that there exists a feature map and a quantum kernel that make VQC and QSVM efficient solvers for any BQP problem. This means that the feature map of VQC or the quantum kernel of QSVM can be designed to have quantum advantage for any classification problem that cannot be classically solved in polynomial time but contrariwise by a quantum computer.

Optimal quantum kernels for small data classification

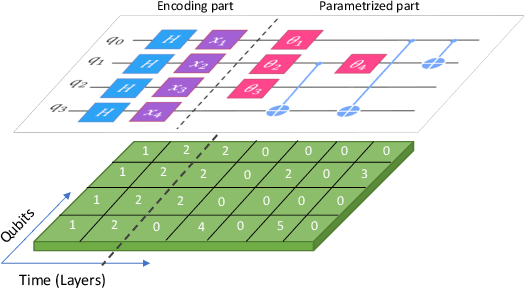
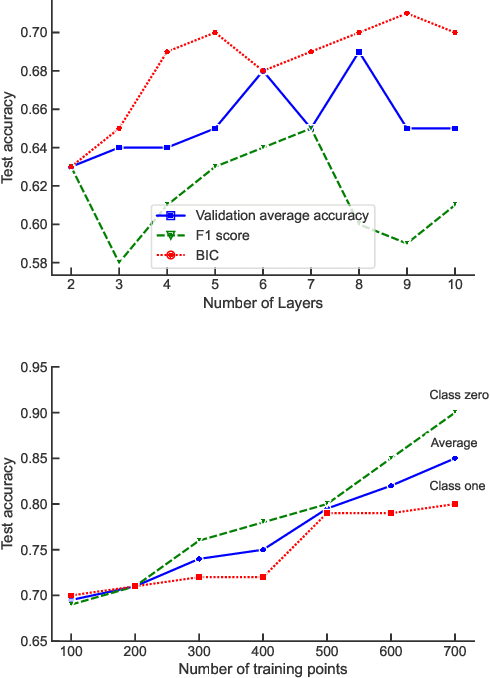
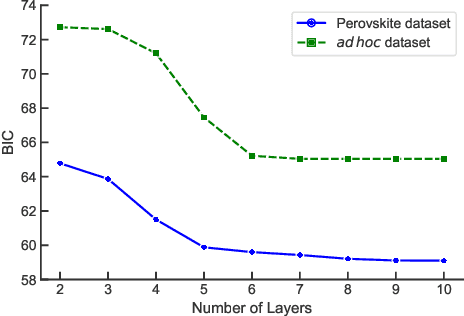
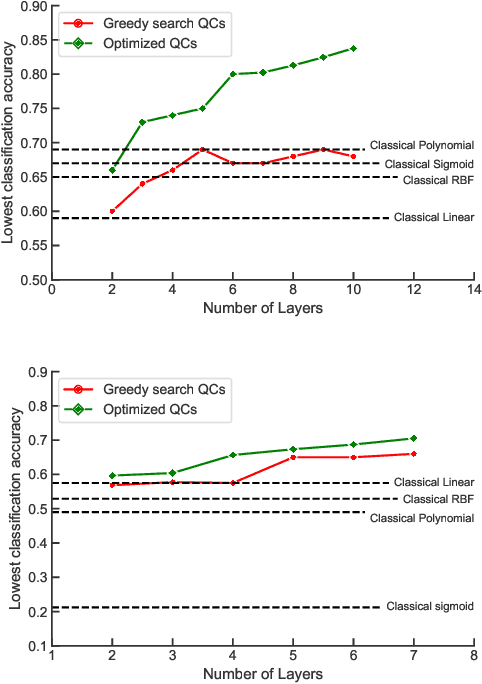
While quantum machine learning (ML) has been proposed to be one of the most promising applications of quantum computing, how to build quantum ML models that outperform classical ML remains a major open question. Here, we demonstrate an algorithm for constructing quantum kernels for support vector machines that adapts quantum gate sequences to data. The algorithm includes three essential ingredients: greedy search in the space of quantum circuits, Bayesian information criterion as circuit selection metric and Bayesian optimization of the parameters of the optimal quantum circuit identified. The performance of the resulting quantum models for classification problems with a small number of training points significantly exceeds that of optimized classical models with conventional kernels. In addition, we illustrate the possibility of mapping quantum circuits onto molecular fingerprints and show that performant quantum kernels can be isolated in the resulting chemical space. This suggests that methods developed for optimization and interpolation of molecular properties across chemical spaces can be used for building quantum circuits for quantum machine learning with enhanced performance.