A case study of sending graph neural networks back to the test bench for applications in high-energy particle physics

In high-energy particle collisions, the primary collision products usually decay further resulting in tree-like, hierarchical structures with a priori unknown multiplicity. At the stable-particle level all decay products of a collision form permutation invariant sets of final state objects. The analogy to mathematical graphs gives rise to the idea that graph neural networks (GNNs), which naturally resemble these properties, should be best-suited to address many tasks related to high-energy particle physics. In this paper we describe a benchmark test of a typical GNN against neural networks of the well-established deep fully-connected feed-forward architecture. We aim at performing this comparison maximally unbiased in terms of nodes, hidden layers, or trainable parameters of the neural networks under study. As physics case we use the classification of the final state X produced in association with top quark-antiquark pairs in proton-proton collisions at the Large Hadron Collider at CERN, where X stands for a bottom quark-antiquark pair produced either non-resonantly or through the decay of an intermediately produced Z or Higgs boson.

Optimal statistical inference in the presence of systematic uncertainties using neural network optimization based on binned Poisson likelihoods with nuisance parameters

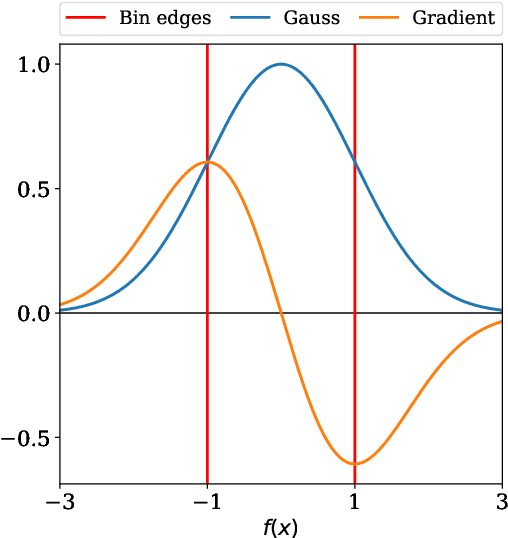
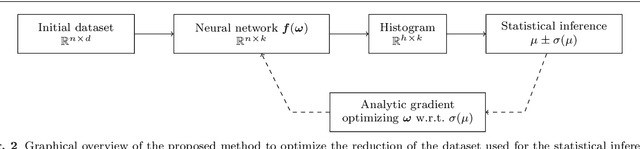
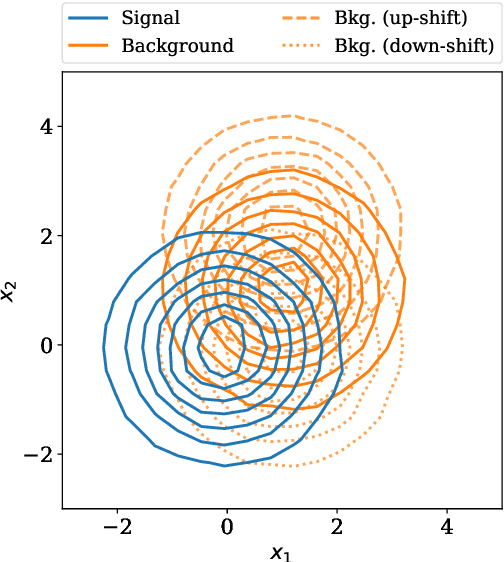
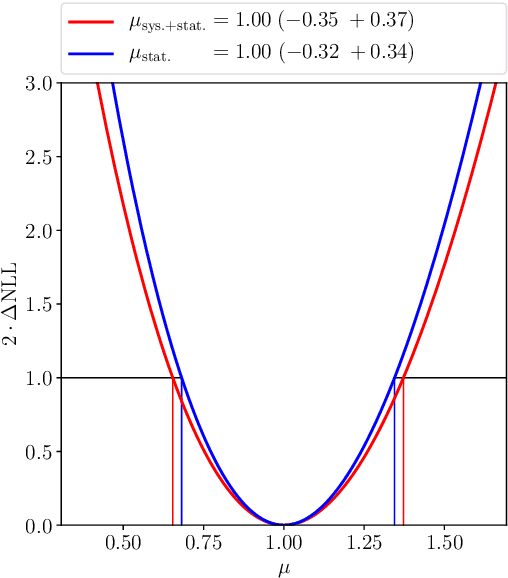
Data analysis in science, e.g., high-energy particle physics, is often subject to an intractable likelihood if the observables and observations span a high-dimensional input space. Typically the problem is solved by reducing the dimensionality using feature engineering and histograms, whereby the latter technique allows to build the likelihood using Poisson statistics. However, in the presence of systematic uncertainties represented by nuisance parameters in the likelihood, the optimal dimensionality reduction with a minimal loss of information about the parameters of interest is not known. This work presents a novel strategy to construct the dimensionality reduction with neural networks for feature engineering and a differential formulation of histograms so that the full workflow can be optimized with the result of the statistical inference, e.g., the variance of a parameter of interest, as objective. We discuss how this approach results in an estimate of the parameters of interest that is close to optimal and the applicability of the technique is demonstrated with a simple example based on pseudo-experiments and a more complex example from high-energy particle physics.