From noisy observables to accurate ground state energies: a quantum classical signal subspace approach with denoising

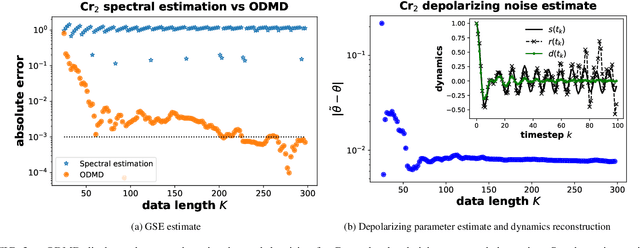
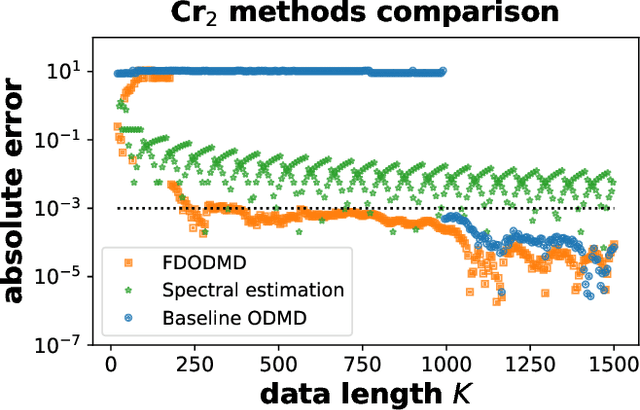
We propose a hybrid quantum-classical algorithm for ground state energy (GSE) estimation that remains robust to highly noisy data and exhibits low sensitivity to hyperparameter tuning. Our approach -- Fourier Denoising Observable Dynamic Mode Decomposition (FDODMD) -- combines Fourier-based denoising thresholding to suppress spurious noise modes with observable dynamic mode decomposition (ODMD), a quantum-classical signal subspace method. By applying ODMD to an ensemble of denoised time-domain trajectories, FDODMD reliably estimates the system's eigenfrequencies. We also provide an error analysis of FDODMD. Numerical experiments on molecular systems demonstrate that FDODMD achieves convergence in high-noise regimes inaccessible to baseline methods under a limited quantum computational budget, while accelerating spectral estimation in intermediate-noise regimes. Importantly, this performance gain is entirely classical, requiring no additional quantum overhead and significantly reducing overall quantum resource demands.

Quantum pixel representations and compression for $N$-dimensional images

We introduce a novel and uniform framework for quantum pixel representations that overarches many of the most popular representations proposed in the recent literature, such as (I)FRQI, (I)NEQR, MCRQI, and (I)NCQI. The proposed QPIXL framework results in more efficient circuit implementations and significantly reduces the gate complexity for all considered quantum pixel representations. Our method only requires a linear number of gates in terms of the number of pixels and does not use ancilla qubits. Furthermore, the circuits only consist of Ry gates and CNOT gates making them practical in the NISQ era. Additionally, we propose a circuit and image compression algorithm that is shown to be highly effective, being able to reduce the necessary gates to prepare an FRQI state for example scientific images by up to 90% without sacrificing image quality. Our algorithms are made publicly available as part of QPIXL++, a Quantum Image Pixel Library.