Discrete Few-Shot Learning for Pan Privacy

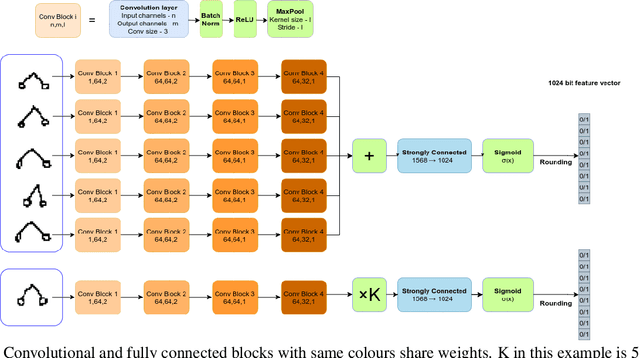
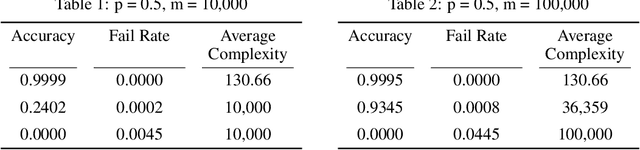
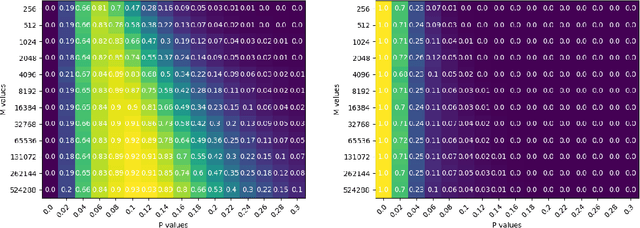
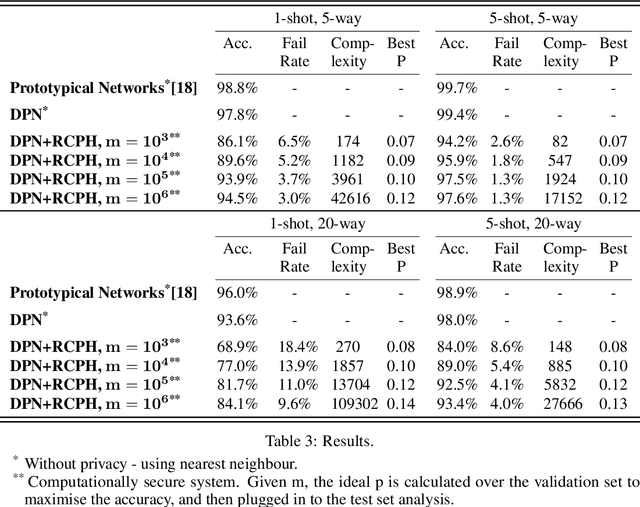
In this paper we present the first baseline results for the task of few-shot learning of discrete embedding vectors for image recognition. Few-shot learning is a highly researched task, commonly leveraged by recognition systems that are resource constrained to train on a small number of images per class. Few-shot systems typically store a continuous embedding vector of each class, posing a risk to privacy where system breaches or insider threats are a concern. Using discrete embedding vectors, we devise a simple cryptographic protocol, which uses one-way hash functions in order to build recognition systems that do not store their users' embedding vectors directly, thus providing the guarantee of computational pan privacy in a practical and wide-spread setting.

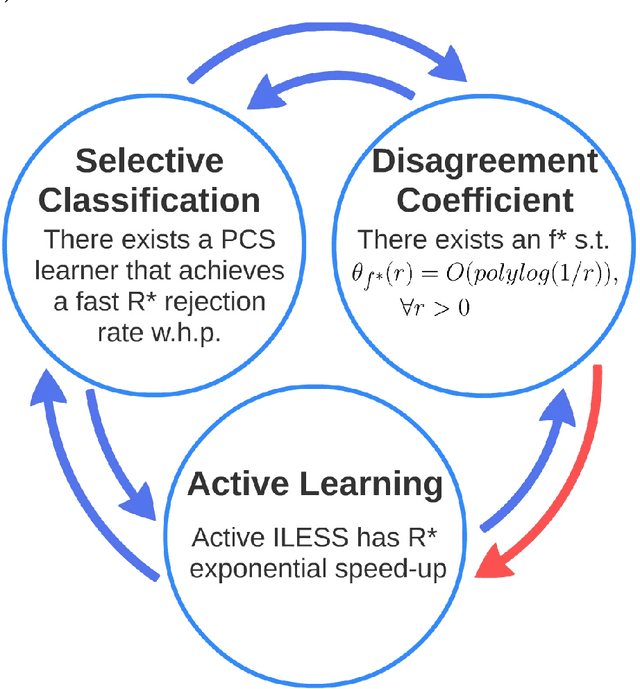
The Relationship Between Agnostic Selective Classification Active Learning and the Disagreement Coefficient

A selective classifier (f,g) comprises a classification function f and a binary selection function g, which determines if the classifier abstains from prediction, or uses f to predict. The classifier is called pointwise-competitive if it classifies each point identically to the best classifier in hindsight (from the same class), whenever it does not abstain. The quality of such a classifier is quantified by its rejection mass, defined to be the probability mass of the points it rejects. A "fast" rejection rate is achieved if the rejection mass is bounded from above by O(1/m) where m is the number of labeled examples used to train the classifier (and O hides logarithmic factors). Pointwise-competitive selective (PCS) classifiers are intimately related to disagreement-based active learning and it is known that in the realizable case, a fast rejection rate of a known PCS algorithm (called Consistent Selective Strategy) is equivalent to an exponential speedup of the well-known CAL active algorithm. We focus on the agnostic setting, for which there is a known algorithm called LESS that learns a PCS classifier and achieves a fast rejection rate (depending on Hanneke's disagreement coefficient) under strong assumptions. We present an improved PCS learning algorithm called ILESS for which we show a fast rate (depending on Hanneke's disagreement coefficient) without any assumptions. Our rejection bound smoothly interpolates the realizable and agnostic settings. The main result of this paper is an equivalence between the following three entities: (i) the existence of a fast rejection rate for any PCS learning algorithm (such as ILESS); (ii) a poly-logarithmic bound for Hanneke's disagreement coefficient; and (iii) an exponential speedup for a new disagreement-based active learner called ActiveiLESS.