Multiphonic modeling using Impulse Pattern Formulation (IPF)

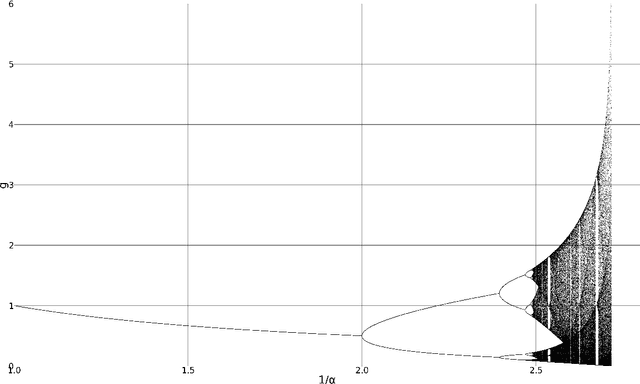
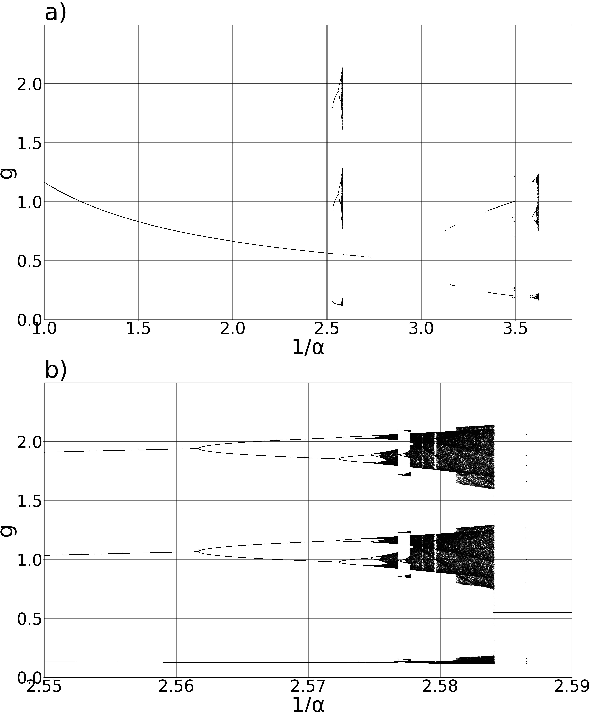
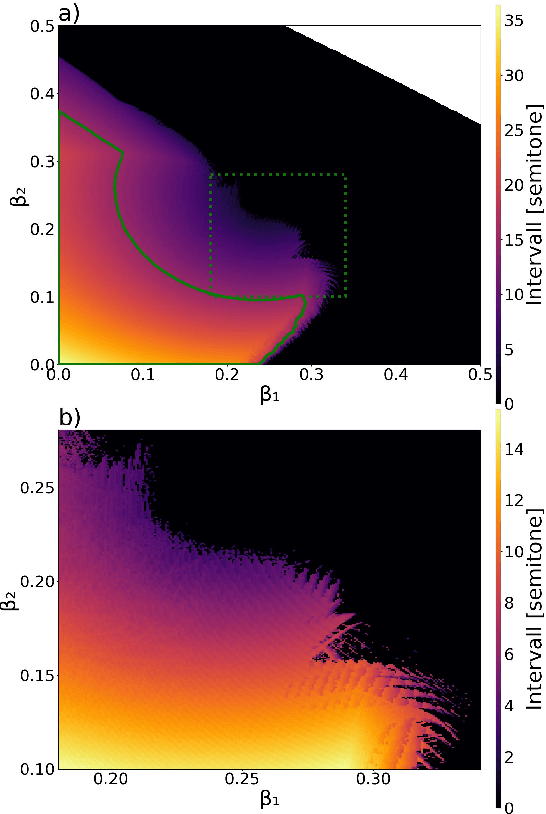
Multiphonics, the presence of multiple pitches within the sound, can be produced in several ways. In wind instruments, they can appear at low blowing pressure when complex fingerings are used. Such multiphonics can be modeled by the Impulse Pattern Formulation (IPF). This top-down method regards musical instruments as systems working with impulses originating from a generating entity, travel through the instrument, are reflected at various positions, and are exponentially damped. Eventually, impulses return to the generating entity and retrigger or interact with subsequent impulses. Due to this straightforward approach, the IPF can explain fundamental principles of complex dynamic systems. While modeling wind instruments played with blowing pressures at the threshold of tone onset, the IPF captures transitions between regular periodicity at nominal pitch, bifurcations, and noise. This corresponds to behavior found in wind instruments where multiphonics appear at the transition between noise and regular musical note regimes. Using the IPF, complex fingerings correspond to multiple reflection points at open finger holes with different reflection strengths. Multiphonics can be modeled if reflection points farther away show higher reflection strength and thus, disrupt periodic motion. The IPF can also synthesize multiphonic sounds by concatenating typical wind instrument waveforms at adjacent impulse time points.

Modeling synchronization in human musical rhythms using Impulse Pattern Formulation (IPF)

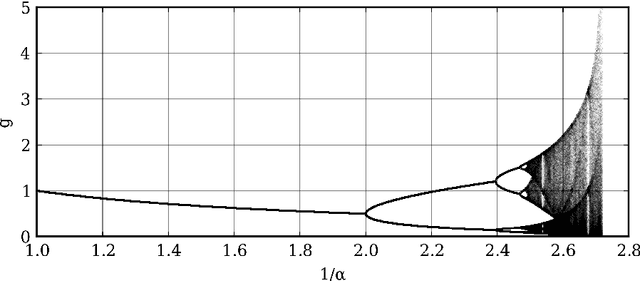
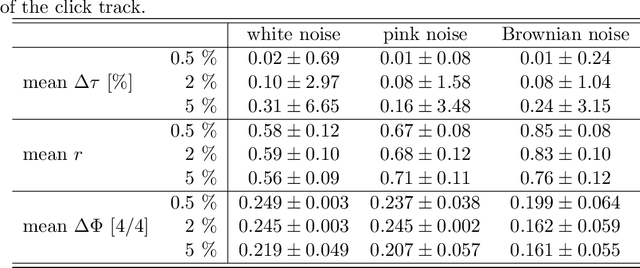
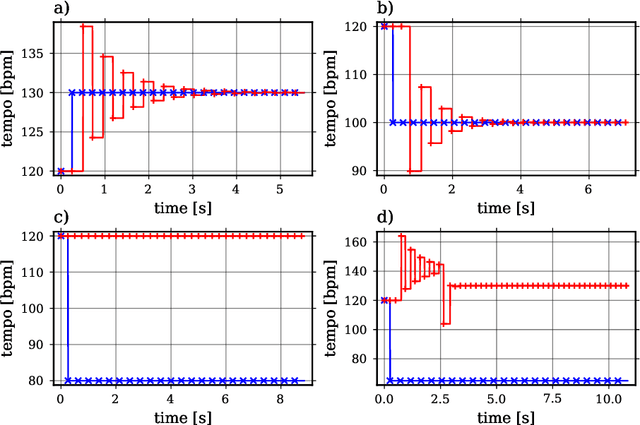
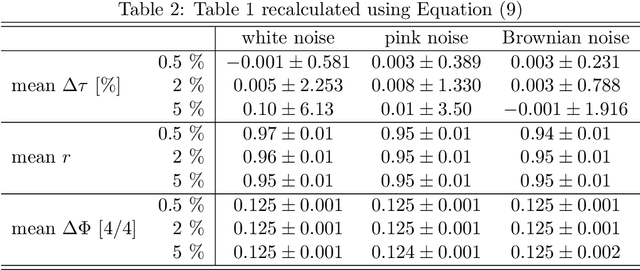
When musicians perform in an ensemble, synchronizing to a mutual pace is the foundation of their musical interaction. Clock generators, e.g., metronomes, or drum machines, might assist such synchronization, but these means, in general, will also distort this natural, self-organized, inter-human synchronization process. In this work, the synchronization of musicians to an external rhythm is modeled using the Impulse Pattern Formulation (IPF), an analytical modeling approach for synergetic systems motivated by research on musical instruments. Nonlinear coupling of system components is described as the interaction of individually propagating and exponentially damped impulse trains. The derived model is systematically examined by analyzing its behavior when coupled to numerical designed and carefully controlled rhythmical beat sequences. The results are evaluated by comparison in the light of other publications on tapping. Finally, the IPF model can be applied to analyze the personal rhythmical signature of specific musicians or to replace drum machines and click tracks with more musical and creative solutions.