Robert Earle
Logical Activation Functions: Logit-space equivalents of Boolean Operators
Oct 22, 2021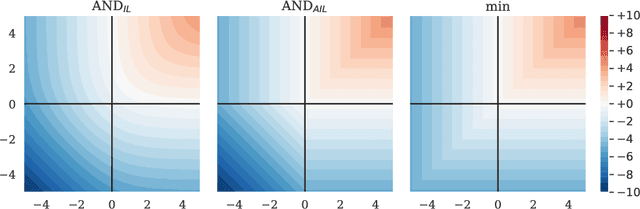
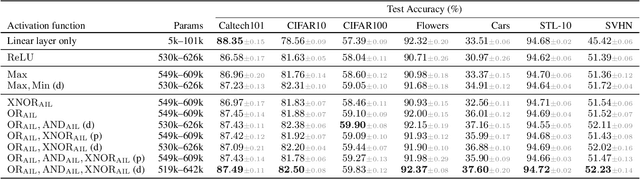
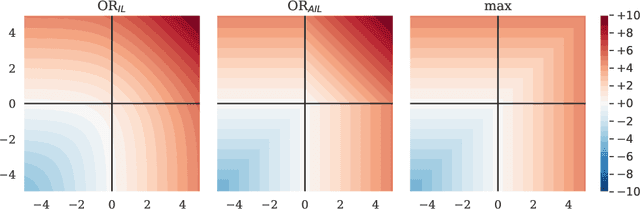

Abstract:Neuronal representations within artificial neural networks are commonly understood as logits, representing the log-odds score of presence (versus absence) of features within the stimulus. Under this interpretation, we can derive the probability $P(x_0 \land x_1)$ that a pair of independent features are both present in the stimulus from their logits. By converting the resulting probability back into a logit, we obtain a logit-space equivalent of the AND operation. However, since this function involves taking multiple exponents and logarithms, it is not well suited to be directly used within neural networks. We thus constructed an efficient approximation named $\text{AND}_\text{AIL}$ (the AND operator Approximate for Independent Logits) utilizing only comparison and addition operations, which can be deployed as an activation function in neural networks. Like MaxOut, $\text{AND}_\text{AIL}$ is a generalization of ReLU to two-dimensions. Additionally, we constructed efficient approximations of the logit-space equivalents to the OR and XNOR operators. We deployed these new activation functions, both in isolation and in conjunction, and demonstrated their effectiveness on a variety of tasks including image classification, transfer learning, abstract reasoning, and compositional zero-shot learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge