Entropy-Guided Sampling of Flat Modes in Discrete Spaces

Sampling from flat modes in discrete spaces is a crucial yet underexplored problem. Flat modes represent robust solutions and have broad applications in combinatorial optimization and discrete generative modeling. However, existing sampling algorithms often overlook the mode volume and struggle to capture flat modes effectively. To address this limitation, we propose \emph{Entropic Discrete Langevin Proposal} (EDLP), which incorporates local entropy into the sampling process through a continuous auxiliary variable under a joint distribution. The local entropy term guides the discrete sampler toward flat modes with a small overhead. We provide non-asymptotic convergence guarantees for EDLP in locally log-concave discrete distributions. Empirically, our method consistently outperforms traditional approaches across tasks that require sampling from flat basins, including Bernoulli distribution, restricted Boltzmann machines, combinatorial optimization, and binary neural networks.

Active Learning for Fair and Stable Online Allocations

We explore an active learning approach for dynamic fair resource allocation problems. Unlike previous work that assumes full feedback from all agents on their allocations, we consider feedback from a select subset of agents at each epoch of the online resource allocation process. Despite this restriction, our proposed algorithms provide regret bounds that are sub-linear in number of time-periods for various measures that include fairness metrics commonly used in resource allocation problems and stability considerations in matching mechanisms. The key insight of our algorithms lies in adaptively identifying the most informative feedback using dueling upper and lower confidence bounds. With this strategy, we show that efficient decision-making does not require extensive feedback and produces efficient outcomes for a variety of problem classes.

Gradient-based Discrete Sampling with Automatic Cyclical Scheduling

Discrete distributions, particularly in high-dimensional deep models, are often highly multimodal due to inherent discontinuities. While gradient-based discrete sampling has proven effective, it is susceptible to becoming trapped in local modes due to the gradient information. To tackle this challenge, we propose an automatic cyclical scheduling, designed for efficient and accurate sampling in multimodal discrete distributions. Our method contains three key components: (1) a cyclical step size schedule where large steps discover new modes and small steps exploit each mode; (2) a cyclical balancing schedule, ensuring ``balanced" proposals for given step sizes and high efficiency of the Markov chain; and (3) an automatic tuning scheme for adjusting the hyperparameters in the cyclical schedules, allowing adaptability across diverse datasets with minimal tuning. We prove the non-asymptotic convergence and inference guarantee for our method in general discrete distributions. Extensive experiments demonstrate the superiority of our method in sampling complex multimodal discrete distributions.

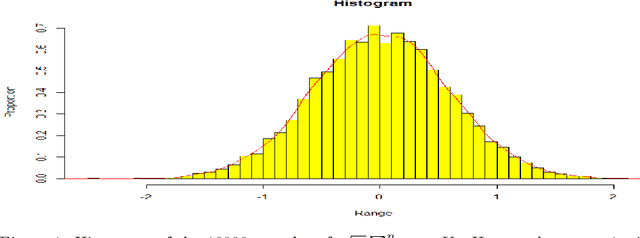
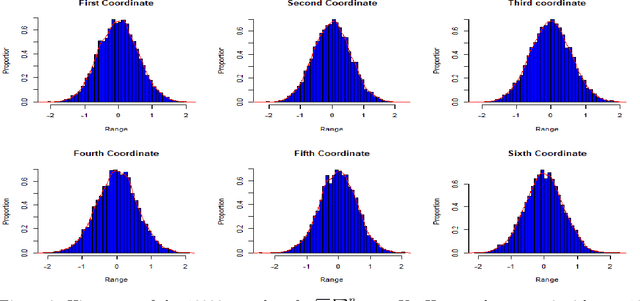
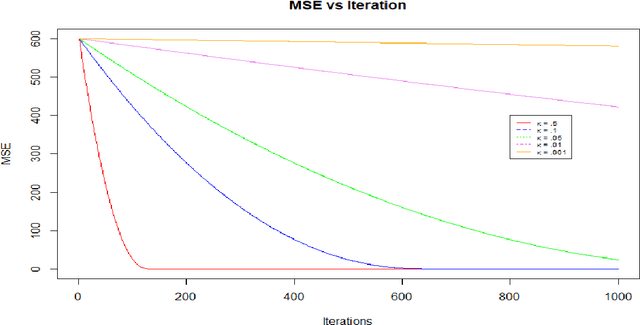
Non Asymptotic Bounds for Optimization via Online Multiplicative Stochastic Gradient Descent

The gradient noise of Stochastic Gradient Descent (SGD) is considered to play a key role in its properties (e.g. escaping low potential points and regularization). Past research has indicated that the covariance of the SGD error done via minibatching plays a critical role in determining its regularization and escape from low potential points. It is however not much explored how much the distribution of the error influences the behavior of the algorithm. Motivated by some new research in this area, we prove universality results by showing that noise classes that have the same mean and covariance structure of SGD via minibatching have similar properties. We mainly consider the Multiplicative Stochastic Gradient Descent (M-SGD) algorithm as introduced by Wu et al., which has a much more general noise class than the SGD algorithm done via minibatching. We establish nonasymptotic bounds for the M-SGD algorithm mainly with respect to the Stochastic Differential Equation corresponding to SGD via minibatching. We also show that the M-SGD error is approximately a scaled Gaussian distribution with mean $0$ at any fixed point of the M-SGD algorithm. We also establish bounds for the convergence of the M-SGD algorithm in the strongly convex regime.