High-dimensional, multiscale online changepoint detection

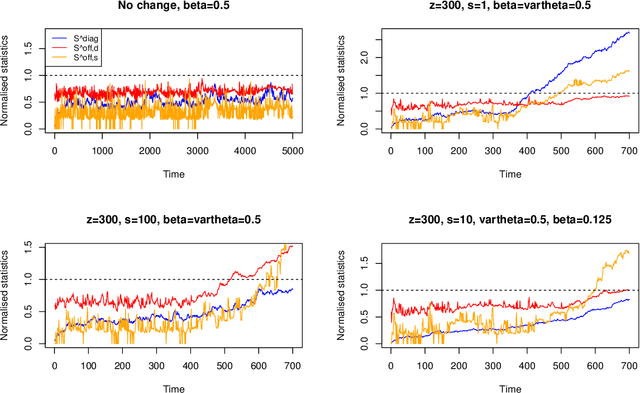
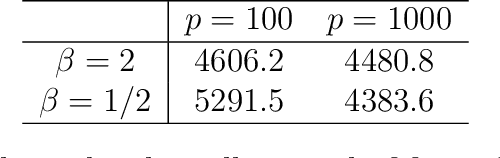
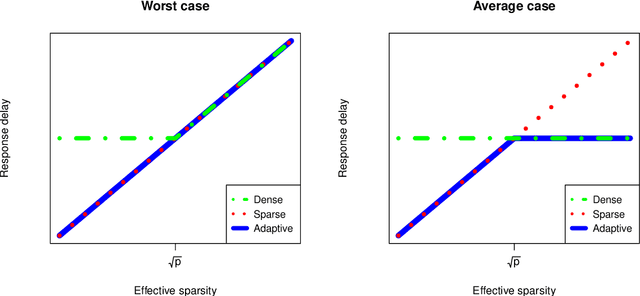
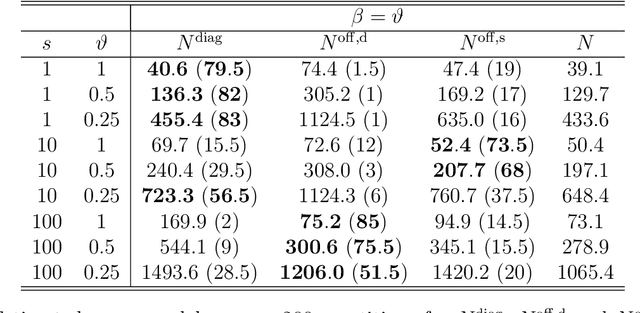
We introduce a new method for high-dimensional, online changepoint detection in settings where a $p$-variate Gaussian data stream may undergo a change in mean. The procedure works by performing likelihood ratio tests against simple alternatives of different scales in each coordinate, and then aggregating test statistics across scales and coordinates. The algorithm is online in the sense that its worst-case computational complexity per new observation, namely $O\bigl(p^2 \log (ep)\bigr)$, is independent of the number of previous observations; in practice, it may even be significantly faster than this. We prove that the patience, or average run length under the null, of our procedure is at least at the desired nominal level, and provide guarantees on its response delay under the alternative that depend on the sparsity of the vector of mean change. Simulations confirm the practical effectiveness of our proposal.

Optimal rates for independence testing via $U$-statistic permutation tests

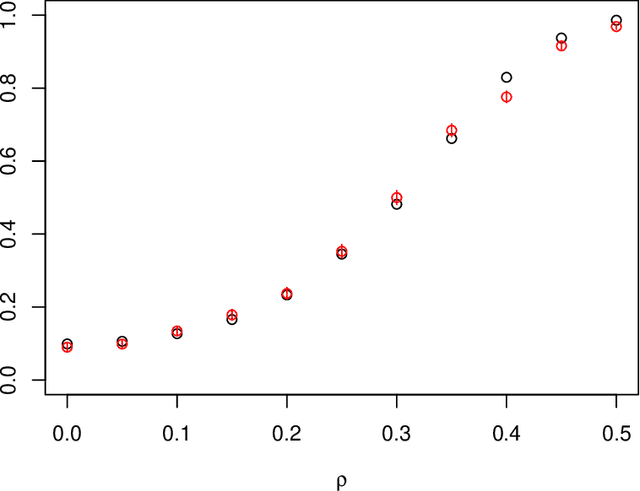
We study the problem of independence testing given independent and identically distributed pairs taking values in a $\sigma$-finite, separable measure space. Defining a natural measure of dependence $D(f)$ as the squared $L_2$-distance between a joint density $f$ and the product of its marginals, we first show that there is no valid test of independence that is uniformly consistent against alternatives of the form $\{f: D(f) \geq \rho^2 \}$. We therefore restrict attention to alternatives that impose additional Sobolev-type smoothness constraints, and define a permutation test based on a basis expansion and a $U$-statistic estimator of $D(f)$ that we prove is minimax optimal in terms of its separation rates in many instances. Finally, for the case of a Fourier basis on $[0,1]^2$, we provide an approximation to the power function that offers several additional insights.

Efficient two-sample functional estimation and the super-oracle phenomenon

We consider the estimation of two-sample integral functionals, of the type that occur naturally, for example, when the object of interest is a divergence between unknown probability densities. Our first main result is that, in wide generality, a weighted nearest neighbour estimator is efficient, in the sense of achieving the local asymptotic minimax lower bound. Moreover, we also prove a corresponding central limit theorem, which facilitates the construction of asymptotically valid confidence intervals for the functional, having asymptotically minimal width. One interesting consequence of our results is the discovery that, for certain functionals, the worst-case performance of our estimator may improve on that of the natural `oracle' estimator, which is given access to the values of the unknown densities at the observations.

Classification with imperfect training labels

We study the effect of imperfect training data labels on the performance of classification methods. In a general setting, where the probability that an observation in the training dataset is mislabelled may depend on both the feature vector and the true label, we bound the excess risk of an arbitrary classifier trained with imperfect labels in terms of its excess risk for predicting a noisy label. This reveals conditions under which a classifier trained with imperfect labels remains consistent for classifying uncorrupted test data points. Furthermore, under stronger conditions, we derive detailed asymptotic properties for the popular $k$-nearest neighbour ($k$nn), support vector machine (SVM) and linear discriminant analysis (LDA) classifiers. One consequence of these results is that the knn and SVM classifiers are robust to imperfect training labels, in the sense that the rate of convergence of the excess risks of these classifiers remains unchanged; in fact, our theoretical and empirical results even show that in some cases, imperfect labels may improve the performance of these methods. On the other hand, the LDA classifier is shown to be typically inconsistent in the presence of label noise unless the prior probabilities of each class are equal. Our theoretical results are supported by a simulation study.

Local nearest neighbour classification with applications to semi-supervised learning

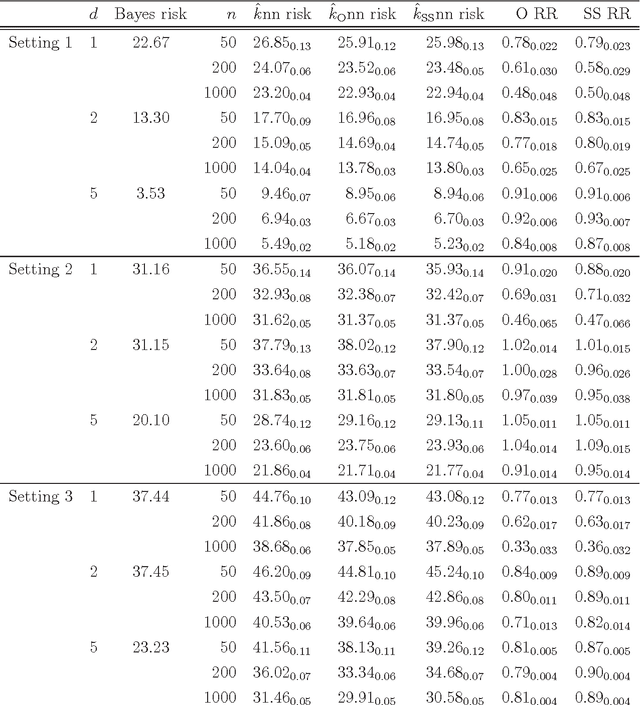
We derive a new asymptotic expansion for the global excess risk of a local $k$-nearest neighbour classifier, where the choice of $k$ may depend upon the test point. This expansion elucidates conditions under which the dominant contribution to the excess risk comes from the locus of points at which each class label is equally likely to occur, but we also show that if these conditions are not satisfied, the dominant contribution may arise from the tails of the marginal distribution of the features. Moreover, we prove that, provided the $d$-dimensional marginal distribution of the features has a finite $\rho$th moment for some $\rho > 4$ (as well as other regularity conditions), a local choice of $k$ can yield a rate of convergence of the excess risk of $O(n^{-4/(d+4)})$, where $n$ is the sample size, whereas for the standard $k$-nearest neighbour classifier, our theory would require $d \geq 5$ and $\rho > 4d/(d-4)$ finite moments to achieve this rate. Our results motivate a new $k$-nearest neighbour classifier for semi-supervised learning problems, where the unlabelled data are used to obtain an estimate of the marginal feature density, and fewer neighbours are used for classification when this density estimate is small. The potential improvements over the standard $k$-nearest neighbour classifier are illustrated both through our theory and via a simulation study.

Sparse principal component analysis via random projections

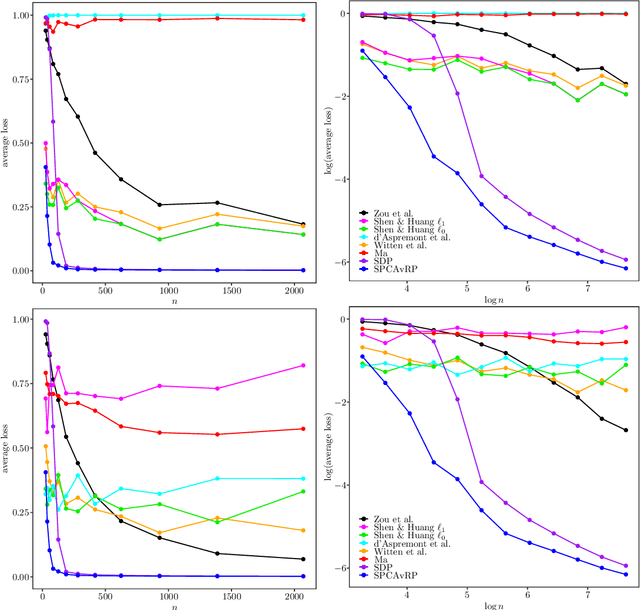
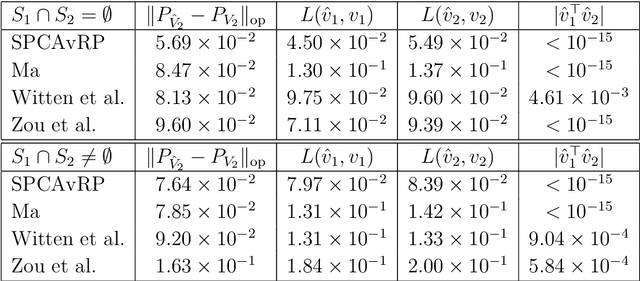
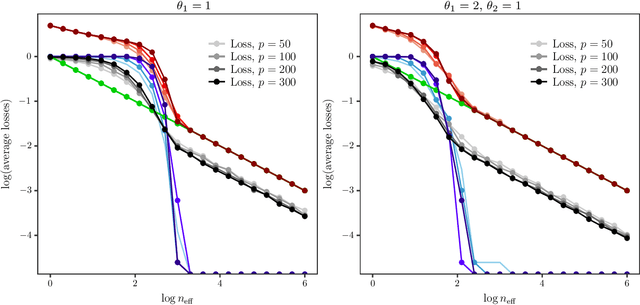
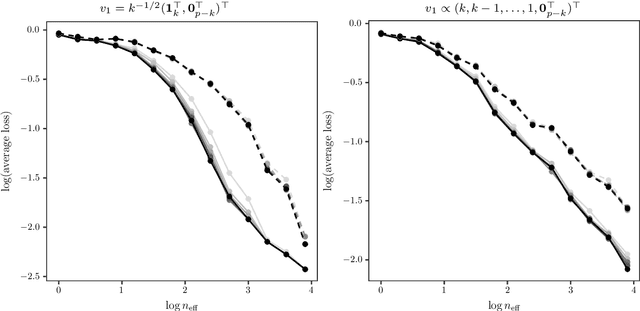
We introduce a new method for sparse principal component analysis, based on the aggregation of eigenvector information from carefully-selected random projections of the sample covariance matrix. Unlike most alternative approaches, our algorithm is non-iterative, so is not vulnerable to a bad choice of initialisation. Our theory provides great detail on the statistical and computational trade-off in our procedure, revealing a subtle interplay between the effective sample size and the number of random projections that are required to achieve the minimax optimal rate. Numerical studies provide further insight into the procedure and confirm its highly competitive finite-sample performance.

Nonparametric independence testing via mutual information

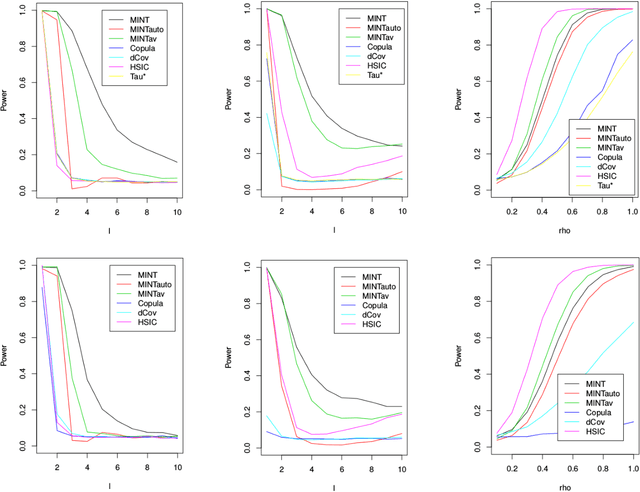
We propose a test of independence of two multivariate random vectors, given a sample from the underlying population. Our approach, which we call MINT, is based on the estimation of mutual information, whose decomposition into joint and marginal entropies facilitates the use of recently-developed efficient entropy estimators derived from nearest neighbour distances. The proposed critical values, which may be obtained from simulation (in the case where one marginal is known) or resampling, guarantee that the test has nominal size, and we provide local power analyses, uniformly over classes of densities whose mutual information satisfies a lower bound. Our ideas may be extended to provide a new goodness-of-fit tests of normal linear models based on assessing the independence of our vector of covariates and an appropriately-defined notion of an error vector. The theory is supported by numerical studies on both simulated and real data.

Statistical and computational trade-offs in estimation of sparse principal components

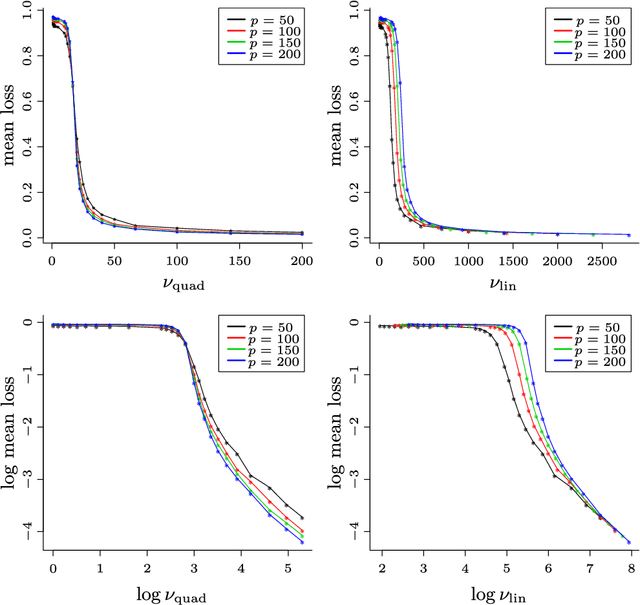
In recent years, sparse principal component analysis has emerged as an extremely popular dimension reduction technique for high-dimensional data. The theoretical challenge, in the simplest case, is to estimate the leading eigenvector of a population covariance matrix under the assumption that this eigenvector is sparse. An impressive range of estimators have been proposed; some of these are fast to compute, while others are known to achieve the minimax optimal rate over certain Gaussian or sub-Gaussian classes. In this paper, we show that, under a widely-believed assumption from computational complexity theory, there is a fundamental trade-off between statistical and computational performance in this problem. More precisely, working with new, larger classes satisfying a restricted covariance concentration condition, we show that there is an effective sample size regime in which no randomised polynomial time algorithm can achieve the minimax optimal rate. We also study the theoretical performance of a (polynomial time) variant of the well-known semidefinite relaxation estimator, revealing a subtle interplay between statistical and computational efficiency.

Choice of neighbor order in nearest-neighbor classification

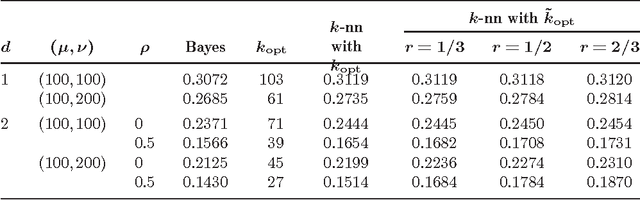
The $k$th-nearest neighbor rule is arguably the simplest and most intuitively appealing nonparametric classification procedure. However, application of this method is inhibited by lack of knowledge about its properties, in particular, about the manner in which it is influenced by the value of $k$; and by the absence of techniques for empirical choice of $k$. In the present paper we detail the way in which the value of $k$ determines the misclassification error. We consider two models, Poisson and Binomial, for the training samples. Under the first model, data are recorded in a Poisson stream and are "assigned" to one or other of the two populations in accordance with the prior probabilities. In particular, the total number of data in both training samples is a Poisson-distributed random variable. Under the Binomial model, however, the total number of data in the training samples is fixed, although again each data value is assigned in a random way. Although the values of risk and regret associated with the Poisson and Binomial models are different, they are asymptotically equivalent to first order, and also to the risks associated with kernel-based classifiers that are tailored to the case of two derivatives. These properties motivate new methods for choosing the value of $k$.