Ricardo Silva
Learning Measurement Models for Unobserved Variables
Oct 19, 2012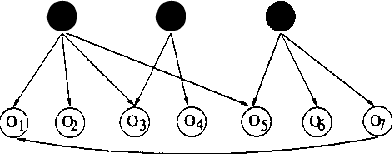
Abstract:Observed associations in a database may be due in whole or part to variations in unrecorded (latent) variables. Identifying such variables and their causal relationships with one another is a principal goal in many scientific and practical domains. Previous work shows that, given a partition of observed variables such that members of a class share only a single latent common cause, standard search algorithms for causal Bayes nets can infer structural relations between latent variables. We introduce an algorithm for discovering such partitions when they exist. Uniquely among available procedures, the algorithm is (asymptotically) correct under standard assumptions in causal Bayes net search algorithms, requires no prior knowledge of the number of latent variables, and does not depend on the mathematical form of the relationships among the latent variables. We evaluate the algorithm on a variety of simulated data sets.
Latent Composite Likelihood Learning for the Structured Canonical Correlation Model
Oct 16, 2012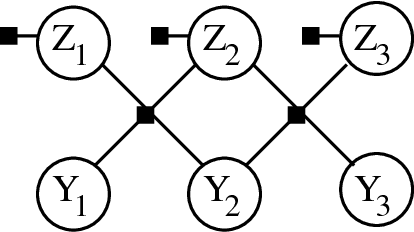
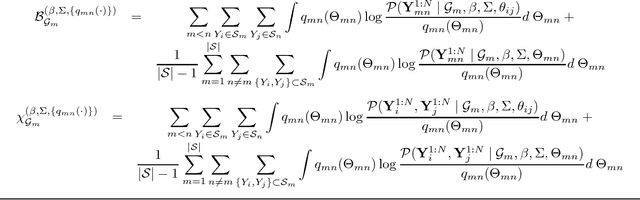
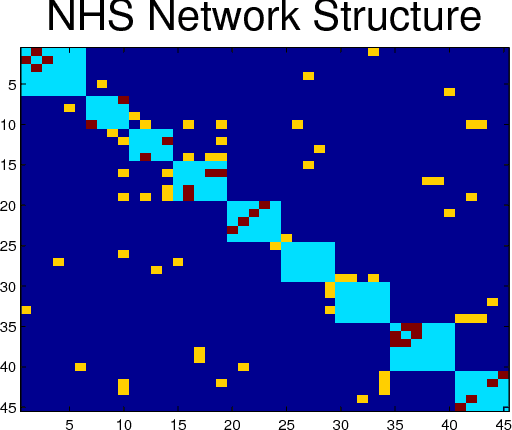
Abstract:Latent variable models are used to estimate variables of interest quantities which are observable only up to some measurement error. In many studies, such variables are known but not precisely quantifiable (such as "job satisfaction" in social sciences and marketing, "analytical ability" in educational testing, or "inflation" in economics). This leads to the development of measurement instruments to record noisy indirect evidence for such unobserved variables such as surveys, tests and price indexes. In such problems, there are postulated latent variables and a given measurement model. At the same time, other unantecipated latent variables can add further unmeasured confounding to the observed variables. The problem is how to deal with unantecipated latents variables. In this paper, we provide a method loosely inspired by canonical correlation that makes use of background information concerning the "known" latent variables. Given a partially specified structure, it provides a structure learning approach to detect "unknown unknowns," the confounding effect of potentially infinitely many other latent variables. This is done without explicitly modeling such extra latent factors. Because of the special structure of the problem, we are able to exploit a new variation of composite likelihood fitting to efficiently learn this structure. Validation is provided with experiments in synthetic data and the analysis of a large survey done with a sample of over 100,000 staff members of the National Health Service of the United Kingdom.
Bayesian Inference for Gaussian Mixed Graph Models
Jun 27, 2012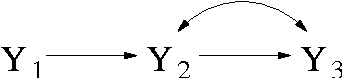
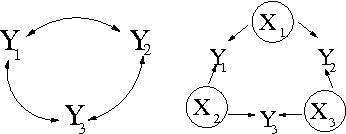
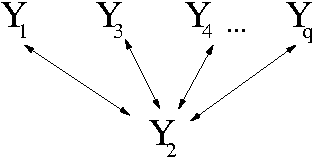
Abstract:We introduce priors and algorithms to perform Bayesian inference in Gaussian models defined by acyclic directed mixed graphs. Such a class of graphs, composed of directed and bi-directed edges, is a representation of conditional independencies that is closed under marginalization and arises naturally from causal models which allow for unmeasured confounding. Monte Carlo methods and a variational approximation for such models are presented. Our algorithms for Bayesian inference allow the evaluation of posterior distributions for several quantities of interest, including causal effects that are not identifiable from data alone but could otherwise be inferred where informative prior knowledge about confounding is available.
Mixed Cumulative Distribution Networks
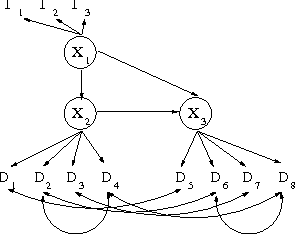
Aug 31, 2010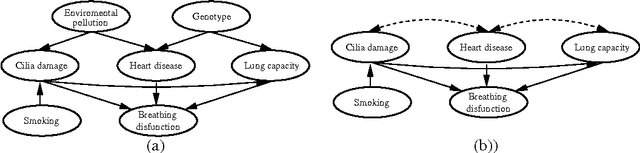

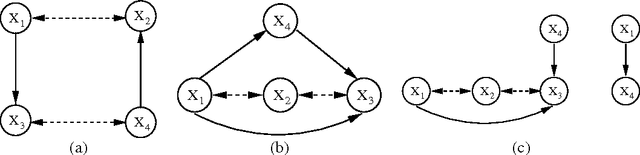
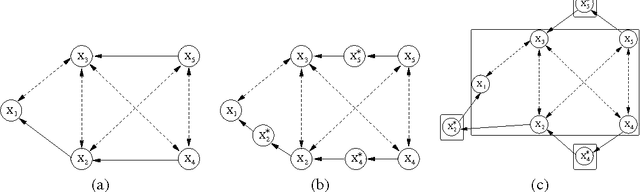
Abstract:Directed acyclic graphs (DAGs) are a popular framework to express multivariate probability distributions. Acyclic directed mixed graphs (ADMGs) are generalizations of DAGs that can succinctly capture much richer sets of conditional independencies, and are especially useful in modeling the effects of latent variables implicitly. Unfortunately there are currently no good parameterizations of general ADMGs. In this paper, we apply recent work on cumulative distribution networks and copulas to propose one one general construction for ADMG models. We consider a simple parameter estimation approach, and report some encouraging experimental results.
Measuring Latent Causal Structure
Jan 07, 2010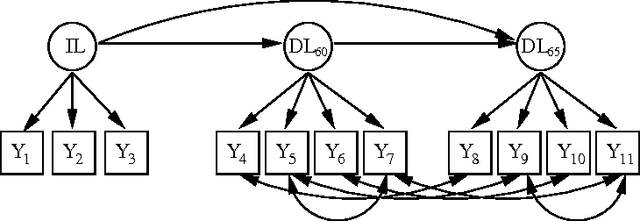
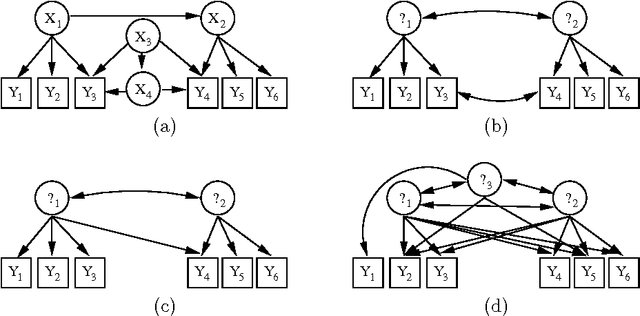
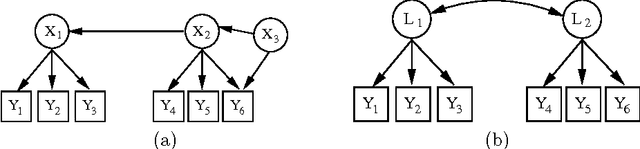
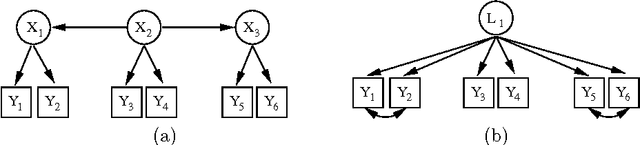
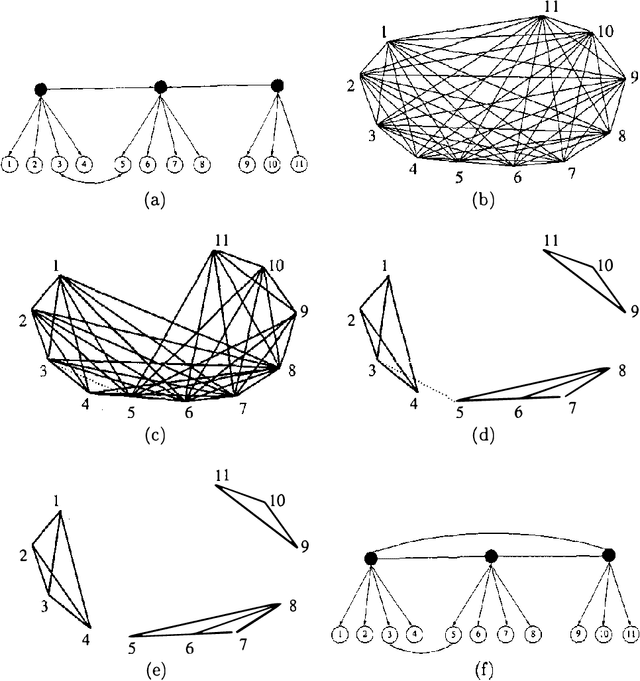
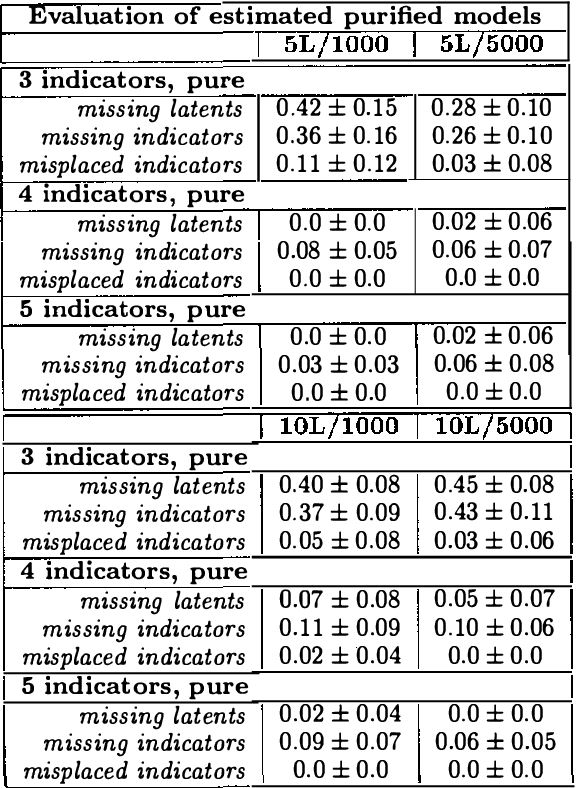
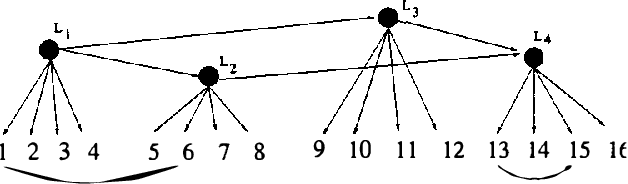
Abstract:Discovering latent representations of the observed world has become increasingly more relevant in data analysis. Much of the effort concentrates on building latent variables which can be used in prediction problems, such as classification and regression. A related goal of learning latent structure from data is that of identifying which hidden common causes generate the observations, such as in applications that require predicting the effect of policies. This will be the main problem tackled in our contribution: given a dataset of indicators assumed to be generated by unknown and unmeasured common causes, we wish to discover which hidden common causes are those, and how they generate our data. This is possible under the assumption that observed variables are linear functions of the latent causes with additive noise. Previous results in the literature present solutions for the case where each observed variable is a noisy function of a single latent variable. We show how to extend the existing results for some cases where observed variables measure more than one latent variable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge